1.参考资料

• Quaternion kinematics for the error-state KF
• barfoot《state estimation forrobotics》
• 袁信、郑锷《捷联式惯性导航原理》
• 以上书籍的下载链接链接：http://pan.baidu.com/s/1c1G0k5U 密码：jdsz

2.旋转矩阵的性质

2.1旋转矩阵

• 定义frame1到frame2的旋转矩阵为，旋转矩阵是单位正交矩阵。

  
  

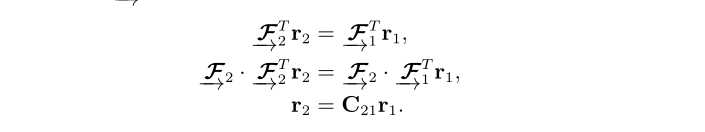
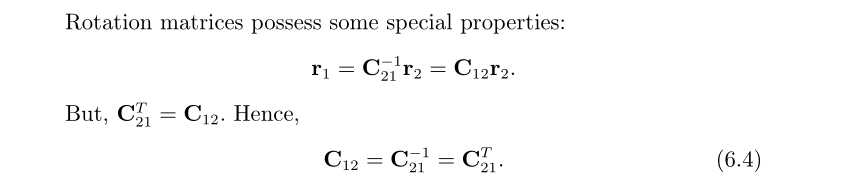
• 对于旋转矩阵的下标可以这样理解，等式右边是旋转矩阵转化后的新位置坐标，左右是上一时刻的位置坐标,因此旋转的叠加（积分）即在原来的基础上再左乘新的旋转矩阵。

  

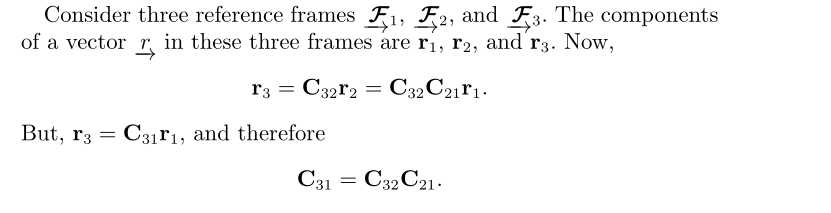
• z-y-x即图中3-2-1，是我看很多导航的书的表示方式，barfoot的书中以1-2-3旋转方式作为航空中常用的旋转方式，对比袁信的捷联惯导书和barfoot的书，两者每次旋转对应的旋转矩阵是相通的，只不过定义的旋转次序不同使得旋转矩阵的形式不太一样
  -欧拉角的大小和方向定义：

  

• barfoot书中每次旋转的旋转矩阵定义，和袁信书中一致。

  
  
  

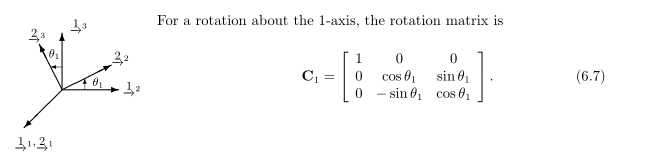
• 以袁信书中的z-y-x即3-2-1的旋转方式表示的旋转矩阵，,这里frame1看作是n系，frame2看作是b系，则导航系n到机体系b的旋转矩阵

  

• 旋转矩阵的小角度表示：当旋转角都比较小时，利用三角函数的与欧拉角的近似,省略小量的二次以上部分，得到：

  

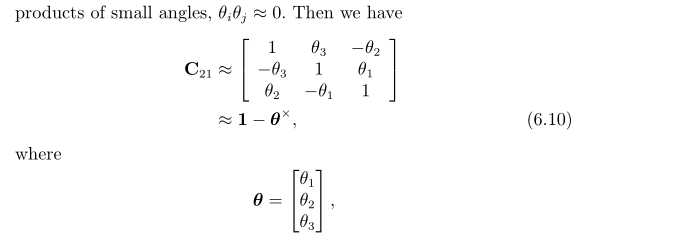
2.2旋转矩阵的奇异点

• barfoot书中以1-2-3的旋转方式为例，如果中间那次旋转，则旋转就会变成绕1轴旋转,即旋转耦合在一起，即这次旋转的欧拉角无法恢复。

  

2.3旋转矩阵的微分方程

• 哥氏定理

  

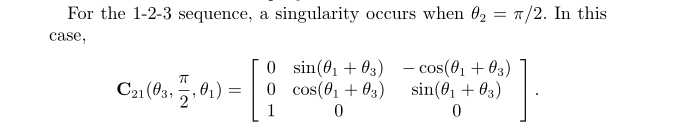
• 利用哥氏定理推导旋转矩阵的微分方程

  
  
  

3.向量叉乘与斜对称矩阵

• 向量叉乘可以表示成向量的叉乘矩阵和向量相乘，叉乘矩阵是斜对称矩阵,这种表示在旋转相关公式里经常用到。对于列向量a,b有：

  

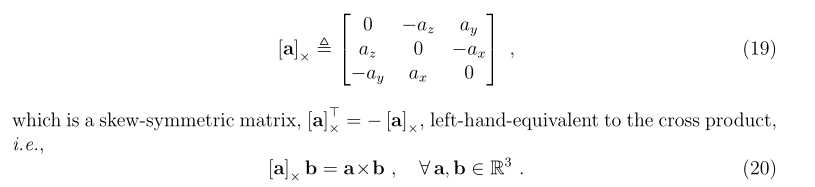
4.四元数

4.1四元数表示

• 四元数有很多表示方法，这里采用标量+向量的形式表示（scalar+vector）

  
  

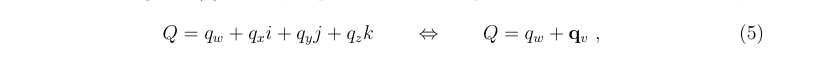
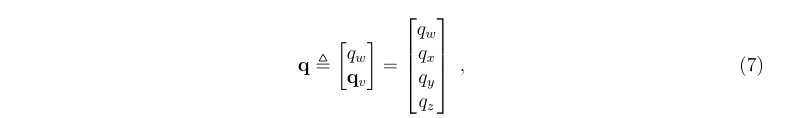
4.2四元数乘法

• 两个四元数等于各个元素分别相乘，表示旋转的积分

  
  

• 四元数乘法不满足交换律(commutative)

  

• 四元数乘法满足结合律(associative)和分配律(distributive)

  

• 两个四元数相乘可以表示为矩阵的形式

  

• 利用四元数的结合律得到

  

4.3四元数的性质

• 单位1 四元数(Identity):

  

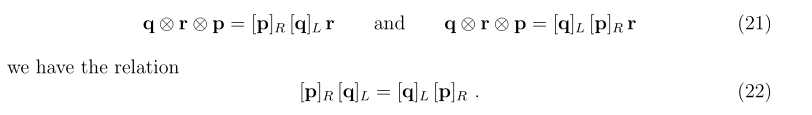
• 共轭四元数：虚数部分符号相反

  

• 单位四元数的逆等于其共轭四元数

  
  

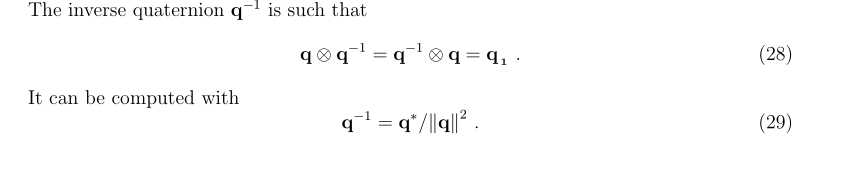
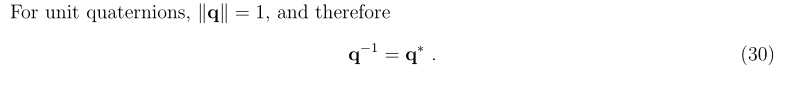
四元数运动学笔记（1）旋转的表示

原文：http://www.cnblogs.com/youzx/p/6327418.html