转自:http://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html
http://blog.csdn.net/google19890102/article/details/45532745
FM原理 =>解决稀疏数据下的特征组合问题,
1) 可用于高度稀疏数据场景;2) 具有线性的计算复杂度
对于categorical(枚举)类型特征,需要经过One-Hot Encoding转换成数值型特征。CTR/CVR预测时,用户的性别、职业、教育水平、品类偏好,商品的品类等,经过One-Hot编码转换后都会导致样本数据的稀疏性。特别是商品品类这种类型的特征,如商品的末级品类约有550个,采用One-Hot编码生成550个数值特征,但每个样本的这550个特征,有且仅有一个是有效的(非零)。由此可见,经过One-Hot编码之后,大部分样本数据特征是比较稀疏的,同时导致特征空间大。
通过观察大量的样本数据可以发现,某些特征经过关联之后,与label之间的相关性就会提高。例如,“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征,对用户的点击有着正向的影响。换句话说,来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为,而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的,如“化妆品”类商品与“女”性,“球类运动配件”的商品与“男”性,“电影票”的商品与“电影”品类偏好等。因此,引入两个特征的组合是非常有意义的。(我的理解:个性化特征)
一般的线性模型为:
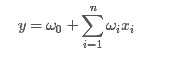
从上面的式子很容易看出,一般的线性模型压根没有考虑特征间的关联。为了表述特征间的相关性,我们采用多项式模型。在多项式模型中,特征xi与xj的组合用xixj表示。为了简单起见,我们讨论二阶多项式模型。具体的模型表达式如下:
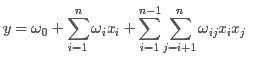
上式中,n表示样本的特征数量,xi表示第i个特征。
与线性模型相比,FM(Factorization Machine)的模型就多了后面特征组合的部分。
从公式(1)可以看出,组合特征的参数一共有 n(n?1)/2 个,任意两个参数都是独立的。然而,在数据稀疏性普遍存在的实际应用场景中,二次项参数的训练是很困难的。其原因是,每个参数 wij 的训练需要大量 xi 和xj都非零的样本;由于样本数据本来就比较稀疏,满足“xi 和 xj 都非零”的样本将会非常少。训练样本的不足,很容易导致参数 wij 不准确,最终将严重影响模型的性能。
为了求出ωij,我们对每一个特征分量xi引入辅助向量Vi=(vi1,vi2,?,vik)。然后,利用vivTj对ωij进行求解。对k值的限定,反映了FM模型的表达能力。
那么ωij组成的矩阵可以表示为:
则FM的模型方程为:
FM算法的求解过程
回归问题:最小均方误差(the least square error)
二分类问题:对数损失函数,其中表示的是阶跃函数Sigmoid
对数损失是用于最大似然估计的,一组参数在一堆数据下的似然值,等于每一条数据的概率之积,而损失函数一般是每条数据的损失之和,为了把积变为和,就取了对数。再加个负号是为了让最大似然值和最小损失对应起来。
对于回归问题:
对于二分类问题:
原文:http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/6340129.html