机器为什么可以学习(1)---测试和训练过程

1、课程内容

　　数据来源于同一分布，且hypothesis 集合有限的情况下，学习是可能的，由PAC准则保证，那么在感知机模型中假设空间是无限的，那么无限hypothesis情况下学习为什么依然还成立？

2、复习，统计学习流程

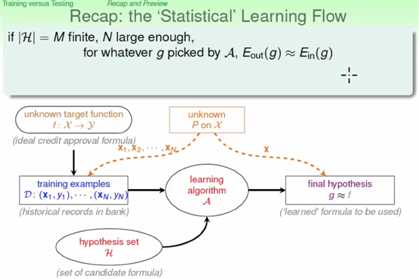
　　上述的流程中分为两部分，一部分是选择一个E_in最小的g作为f，另一个过程就是测试这个g以测试数据集上的表现：

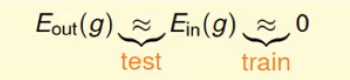
　　学习的两个核心问题：

　　对于这两个核心问题，hypothesis 集合的大小对这两问题的有什么关键的作用？

　　对于小的M来说，第一个问题的答案很好，有多hypothesis的霍夫曼不等式可以M越小，那么发生坏事情（E_in和E_out不接近)的概率就越小，但是对于第二个问题来说，M越小选择就越少，可能不会使得E_in很小；

　　对于大的M来说，同样有霍曼夫不等式可知，发生坏事情的概率变大，但是对于第二问题来说，选择足够多。也就是说选择M的大小是对上面的核心问题是有很大影响的，那么当M无限大的时候会是什么情况？能不能使用一个有限的m_H替代霍夫曼中的M，使得M在无穷时霍夫丁不等式依然成立。

2、M从哪里来？

　　多hypothesis下的霍夫丁不等式：其中M是hypothesis的个数；

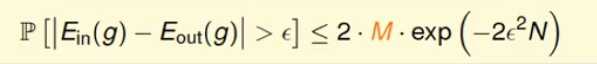
　　M通过union bound得到，某样本在所有的hypothesis上发生不好的概率上限P[B₁ or B₂ or .......B_M]是：

　　通过以上分析可知，M来自于union bound操作，现分析一下union bound是否合理？

　　对于假设空间中的假设函数有很多是类似的，那么就是说E_in(h₁) ≈ E_in(h₂)，在训练数据集上发生不好的概率应该也是有关系的h₁不好的话，h₂不好的概率也很大，也就是说union bound的上限扩的太大了；

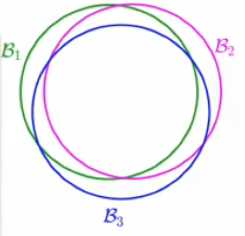
　　over-estimating就造成了union bound失败，怎么解决这个over-estimating的问题？找到重叠的部分，对相似的hypothesis进行按组分类：

3、hypothesis的分类

　　待分类的hypothesis集合：

　　对于该集合的hypothesis有无穷多个，那么针对该假设空间可以怎么分类？假如数据集只有一个数据输入x₁

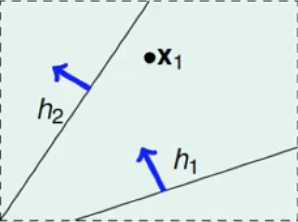
　　此时从数据x₁的角度来说，整个hypothesis空间只用两种不同的分类：

　　；

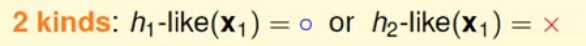　　假设数据只有两个的情况下：

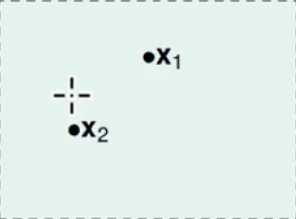
　　当只有两个数据的时候那么总共会有4中分类：

　　同理，当有3个数据时，总共有8种分类，因此可以发现这样的规律，对于0/1分类来说，每个点要不是O要不是X因此在有N个数据时hypothesis集合的函数分类最多为2^N次方个；

　　总之，当输入数据有N个时，假设空间中的无限个函数可以分成种类为effective(N)，则有：

　　(1)、effective(N) <= 2N

　　(2)、无限种类的hypothesis可以分成有限的种类

　　(3)、因此多hypothesis的霍夫丁不等式可以进一步的精确为：

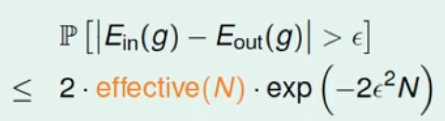
　　如果effective(N)可以替代N，并且effective(N)要远小于2^N，那么在无限个hypothesis空间下的学习就是可能的，下节课进行讨论这一问题。

机器为什么可以学习(1)---测试和训练过程

原文：http://www.cnblogs.com/daguankele/p/6345103.html