| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 8636 | Accepted: 4105 |
Description
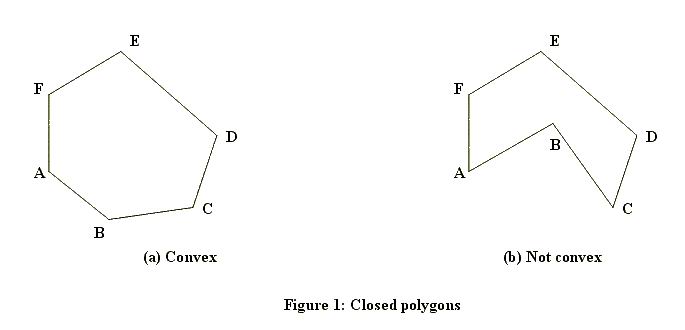
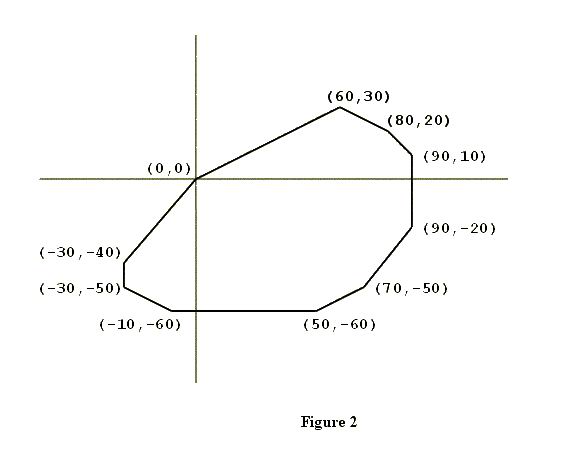
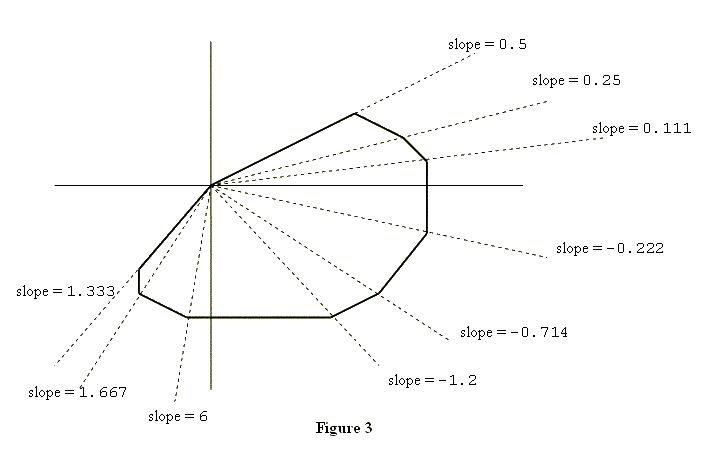
Input
Output
Sample Input
0 0 70 -50 60 30 -30 -50 80 20 50 -60 90 -20 -30 -40 -10 -60 90 10
Sample Output
(0,0) (-30,-40) (-30,-50) (-10,-60) (50,-60) (70,-50) (90,-20) (90,10) (80,20) (60,30)
Source
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> using namespace std; typedef long long ll; const int N=55; const double eps=1e-8; inline int read(){ char c=getchar();int x=0,f=1; while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1; c=getchar();} while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘; c=getchar();} return x*f; } inline int sgn(double x){ if(abs(x)<eps) return 0; else return x<0?-1:1; } struct Vector{ double x,y; Vector(double a=0,double b=0):x(a),y(b){} }; typedef Vector Point; double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;} double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;} int n,x,y; Point p[N],S; bool cmpPolar(Point a,Point b){ return sgn(Cross(a,b))>0; } int main(int argc, const char * argv[]) { while(scanf("%d",&x)!=EOF){ y=read(); p[++n]=Point(x,y); } sort(p+2,p+1+n,cmpPolar); for(int i=1;i<=n;i++) printf("(%.0f,%.0f)\n",p[i].x,p[i].y); return 0; }
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <vector> using namespace std; typedef long long ll; const int N=55; const double eps=1e-8; const double pi=acos(-1); inline int read(){ char c=getchar();int x=0,f=1; while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1; c=getchar();} while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘; c=getchar();} return x*f; } inline int sgn(double x){ if(abs(x)<eps) return 0; else return x<0?-1:1; } struct Vector{ double x,y; Vector(double a=0,double b=0):x(a),y(b){} bool operator <(const Vector &a)const{ //return x<a.x||(x==a.x&&y<a.y); return sgn(x-a.x)<0||(sgn(x-a.x)==0&&sgn(y-a.y)<0); } }; typedef Vector Point; Vector operator +(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);} Vector operator -(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);} Vector operator *(Vector a,double b){return Vector(a.x*b,a.y*b);} Vector operator /(Vector a,double b){return Vector(a.x/b,a.y/b);} bool operator ==(Vector a,Vector b){return sgn(a.x-b.x)==0&&sgn(a.y-b.y)==0;} double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;} double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;} double DisPP(Point a,Point b){ Point t=b-a; return sqrt(t.x*t.x+t.y*t.y); } int ConvexHull(Point p[],int n,Point ch[]){//cannot handle repeat point sort(p+1,p+1+n); int m=0; for(int i=1;i<=n;i++){ while(m>1&&sgn(Cross(ch[m]-ch[m-1],p[i]-ch[m-1]))<=0) m--; ch[++m]=p[i]; } int k=m; for(int i=n-1;i>=1;i--){ while(m>k&&sgn(Cross(ch[m]-ch[m-1],p[i]-ch[m-1]))<=0) m--; ch[++m]=p[i]; } if(n>1) m--;//the first point return m; } int n,x,y; double ans; Point p[N],ch[N]; int main(int argc, const char * argv[]) { while(scanf("%d",&x)!=EOF){ y=read(); p[++n]=Point(x,y); } ConvexHull(p,n,ch); Point S(0,0);int p; for(p=1;p<=n;p++) if(ch[p]==S) break; for(int i=p;i<=n;i++) printf("(%.0f,%.0f)\n",ch[i].x,ch[i].y); for(int i=1;i<p;i++) printf("(%.0f,%.0f)\n",ch[i].x,ch[i].y); return 0; }
POJ 2007 Scrambled Polygon [凸包 极角排序]
原文:http://www.cnblogs.com/candy99/p/6354351.html