我有个朋友有算法强迫症,每次一看到别人写的算法,就有上去改的冲动,不然就会偏头疼,主要症结在于他认为别人写的算法不好,但是什么的算法可以评判为好,什么样的算法可以评判为不好?最近为了治愈他,我特地写了这篇文章。
算法的衡量从两个方向出发:时间复杂度和空间复杂度。本文主要是不讲具体算法,只将算法的衡量,重点讲解如何衡量算法的复杂度,解决平时见到的XX算法时间复杂是O(logn)O(logn),其中这个结果是怎么推导出来的?lognlogn是个什么玩意儿?,大写的OO是什么意思?为什么用这个符号表示等类似问题。
在开始讲解复杂度之前我们先因为一个数学概念Big O notation
Big O notation是一种描述述函数渐进行为的理论,又被称作Landau’s symbol,其实这部分是高数中的概念。用于表述一个函数增长的多快或者减少的多快。(重点描述加速度),在计算机领域,Big O notation常常用来表达算法时间复杂度和性能的术语,一个算法在执行过程中需要的最大时间或者最大空间。
那么为什么要用O来表示呢?
大O符号是由德国数论学家保罗·巴赫曼(Paul Bachmann)在其1892年的著作《解析数论》(Analytische Zahlentheorie)首先引入的。而这个记号则是在另一位德国数论学家艾德蒙·朗道(Edmund Landau)的著作中才推广的,因此它有时又称为朗道符号(Landau symbol)。代表“order of …”(……阶)的大O,最初是一个大写的希腊字母’Θ’(Omicron),现今用的是英文大写字母’O’,但从来不是阿拉伯数字’0’。
(定义这个东西我觉得还是原汁原味的好,犹豫了很久还是决定保留原版)
If we write f(n) = O(g(n)), then there exists a function f(n) such that ? n ≥ n0, f(n) ≤ cg (n) with any constant c and a positive integer n0. Or f(n) = O(g(n)) means we can say g(n) is an asymptotic upper bound for f(n).
If f1(n) is O(g1(n)) and f2(n) is O(g2(n)), then f1(n) + f2(n) is O(max(g1(n), g2(n)))
Transitive Property: If f(n) = O(g(n)) and g(n) is O(h(n)), then f(n) = O(h(n)).
解决一个规模为 n 的问题所花费的时间(或者所需步骤的数目)可以被求得:
当 n 增大到非常大时,n2n2; 项将开始占主导地位,而其他各项可以被忽略(可以参见上面的特性),所以我们可以将T(n)T(n)的渐进函数记O(n2)O(n2),至于上面的公式T(n)T(n)是怎么推导推导出来的,我在下面的篇幅中会细讲。
所有这些函数都处于 N 趋近于无穷大的情况下,增长得慢的函数列在上面。 c 是一个任意常数。
| 符号 | 描述 |
|---|---|
| O(1)O(1) | 常数,表示无论输入是什么,所需要的执行时间(空间都不变)。 |
| O(N)O(N) | 线性,表示随着输入的增加,所需的执行时间(空间)也线程增加。 |
| O(N2)O(N2) | 平方,表示输入的增加,所需要是执行时间(空间)按照平方比例增加。 |
| O(log?N)O(log?N) | 即表示迭代对数,是目前增长最慢的函数 |
| O(logN)O(logN) | 对数 |
| O(N?logN)O(N?logN) | 是线性函数及对数函数相乘的结果 |
| O(Nc),Integer(c>1)O(Nc),Integer(c>1) | 多项式,有时叫作“代数”(阶) |
| O(cN)O(cN) | 指数,有时叫作“几何”(阶) |
| O(N!)O(N!) | 阶乘,有时叫做“组合”(阶) |
在开始正式的引入的算法的复杂度之前,我们来聊聊算法的期望与可解性,我们还是从例子还是讲起
如果我们有一个电话本,这个电话本假设是无序的,电话本中有1000个人的电话,加入我们想找到 “张三”的电话,那么
最好情况(Best Case):O(1)
期望情况(Expected Case):O(n)(对应500)
最坏情况(Worst Case):O(n)(对应1000)
最好的情况就是第一个就是“张三“,非常幸运,最差劲的情况,我们找到第1000个才找到,期望的情况就是在中间找到。衡量一个算法往往都是在探讨期望的情况和最快的情况,因为最好的情况意义不大。
我们依然从一个例子开始讲起:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短(这就是经典的旅行商的问题)
假设有3个城市A、B、C,那就有6中可能(其中3个重复的),即:A->B->C;C->B->A; A->C->B;B->C->A;B->A->C;C->A->B;
实际就是一个阶乘的问题N!N!,如果有5个城市,那么会增加到60中可能,如果增加到10000个城市,这个用一般的电脑已经算不出结果了
虽然你可以写出算法,但是在你的有生之年可能看不到结果了。
那么为什么要谈这块内容呢?,因为有些算法之所以安全就是建立在可解性的基础上的。公钥加密是个极好例子。至于公钥是什么,可以参考我之前的文章《【密码学】一万字带您走进密码学的世界(下)》,自然界中找到一个很大的数的两个素因子是困难的,如果不困难,公钥系统将彻底不安全,建立在公钥的上的应用HTTPS,SSH,BITCOIN等将一块玩完。
每个算法需要一定量的计算机时间来执行其指令和任务。所需的计算机时间称为时间复杂度。算法的时间复杂度可以定义如下。
算法的时间复杂度是算法完成其执行所需的总时间量
语句的执行时间=语句的执行次数(即频度(Frequency Count))×语句执行一次所需时间。
语句执行一次所需时间有多重因素决定,如:
1.算法是运行性单处理器机器上还是在多处理器机器上
2.运行的机器是32位还是64位
3.运行机器的读写速度
4.输出数据量的大小
由此可见,语句执行的时间我们很难真实的估计,因为我们在对比算法的好坏,我们假设是运行在一样的环境中的,实际我们要比较的就是,语句的执行次数,我们从上面的分析可以得到一个结论: 求算法是时间复杂度可类比为求指特性环境下算法的算法的执行次数
现在我们开始回答第二个问题,如何求解算法的时间复杂度?我们依然从例子开始说起,
首先讲的是简单的求和法:
|
1
2
3
4
5
6
7
8
|
int sum(int A[], int n)
{
int sum = 0, i;
for(i = 0; i < n; i++)
sum = sum + A[i];
return sum;
}
|
对于上面的代码,时间复杂度的计算过程如下:
在上面的计算中,Cost表示单条操作所需耗费的计算机时间,Repeatation表示每条操作所重复的次数,Total表示每个操作最终耗费的时间。因为上面需要4n+4个计算机执行时间单元,从上面的Big O notation定理我们可以得到T(n) = O(N),当然这里讲的只是相对简单的求和法的例子。
然后我们看一个稍微复杂点的求和的例子,形如下面代码:
|
1
2
3
4
5
6
7
|
for(in i = 1;i<=n;i++){
for(j=1;j<=j;j++){
for(int k = 1;i< = j;k++){
++x;
}
}
}
|
有上面的Big O notation定理我们知道,我们在考虑的复杂度的时候,小的影响系数可以抛弃掉,因为我们可直接评估++x的执行次数。
$$f(n) = \sum{i=1}^n\sum{j=1}^i\sum{k=j}^m1=\sum{i=1}^n\sum{j=1}^ij=\sum{i=1}^n { \frac{(i+1)}{3} } = \frac {n(n+1)(n+2)}{6}$$
因此上面的时间复杂度为$O(N^3)$
下面我们来看一个有挑战性的例子:
|
1
2
3
4
5
|
i=s=0;
while(s<n){
i++;
s=s+i;
}
|
我们假设循环执行了k次,则有
k=1时,i=1,s=0+1
k=2时,i=2,s=0+1+2
k=3时,i=3,s=0+1+2+3
…
k=k时,i=k,s=0+1+2+3+ …+k = k(k+1)\2
由于循环的条件是s\<n,因此
可以计算出:
所有最终的算法时间复杂度T(n)=O(n??√)T(n)=O(n)
形如下面的代码
|
1
2
3
4
|
int i=1;
while (i<=n){
i=i*2;
}
|
求解:
所以程序最多能执行的次数为 $log2^n,所以时间复杂度为,所以时间复杂度为O(log^n),可能有人会好奇这个结果是怎么得到的。现在问题中的对数可以是,可能有人会好奇这个结果是怎么得到的。现在问题中的对数可以是ln(底数为e),(底数为e),log{10},,log_2或者以其它为底数,这无关紧要,它仍然是或者以其它为底数,这无关紧要,它仍然是O(log^n),正如,正如O(2n^2)和和O(100n^2)都记为都记为O(n^2)$。
|
1
2
3
4
5
6
|
for(i=1;i<=n;i++){ n+1次
for(j=1;j<=n;j++){ n的平方次
sum++; n的平方次
}
}
|
结果:f(n)=n+1+n2+n2=2n2+n+1=O(n2)f(n)=n+1+n2+n2=2n2+n+1=O(n2)
当我们设计一个算法来解决一个问题,它需要一些计算机内存来完成其执行。对于任何算法,内存需要以下用途…
1.存储程序指令所需的内存
2.存储常量值所需的内存
3.存储变量值所需的内存
3.和其他一些东西
算法的空间复杂度可以定义如下:
算法完成其执行所需的计算机存储器的总量被称为该算法的空间复杂度
通常,当程序正在执行时,它使用计算机内存有三个原因。它们如下…
1.指令空间:用于存储已编译版本指令的内存量。
2.环境堆栈:在函数调用时存储部分执行函数信息的内存量。
3.数据空间:用于存储所有变量和常量的内存量。
要计算空间复杂性,我们必须知道存储不同数据类型值所需的内存(根据编译器)。例如,C编程语言编译器需要以下…
1.2字节存储整数值
2.4个字节存储浮点值
3.1个字节存储字符值
4.8个字节存储双精度值
|
1
2
3
|
int square(int a){
return a*a;
}
|
在上面的代码中,它需要2字节的内存来存储变量a,而另一个2字节的内存用于返回值。这意味着,它完全需要4字节的内存来完成其执行。这4字节的内存是固定的任何输入值 a 。这种空间复杂性被认为是恒定的空间复杂性。如果任何算法对于所有输入值需要固定量的空间,则该空间复杂度被称为恒定空间复杂度
|
1
2
3
4
5
6
7
|
int sum(int A[], int n){
int sum = 0, i;
for(i = 0; i < n; i++){
sum = sum + A[i];
return sum;
}
}
|
在上面的代码中需要 n*2 字节存储数组变量的内存a[],2字节的整数参数n内存,4字节的内存为本地整数变量sum和i,返回值的2字节内存。这意味着,完全需要的2n + 8字节的内存来完成其执行。在这里,内存的数量取决于n的输入值。这种空间复杂度称为线性空间复杂度。如果算法所需的空间量随输入值的增加而增加,则空间复杂度称为线性空间复杂度。
最后我们聊聊什么样的算法才是好算法。我想这个我就细讲了,因为下面的图已经很清楚了,需要说明的是,在多数情况下时间复杂度和空间复杂度是相悖的,很多时候提速上来了你却牺牲了空间(比如很多缓存策略)。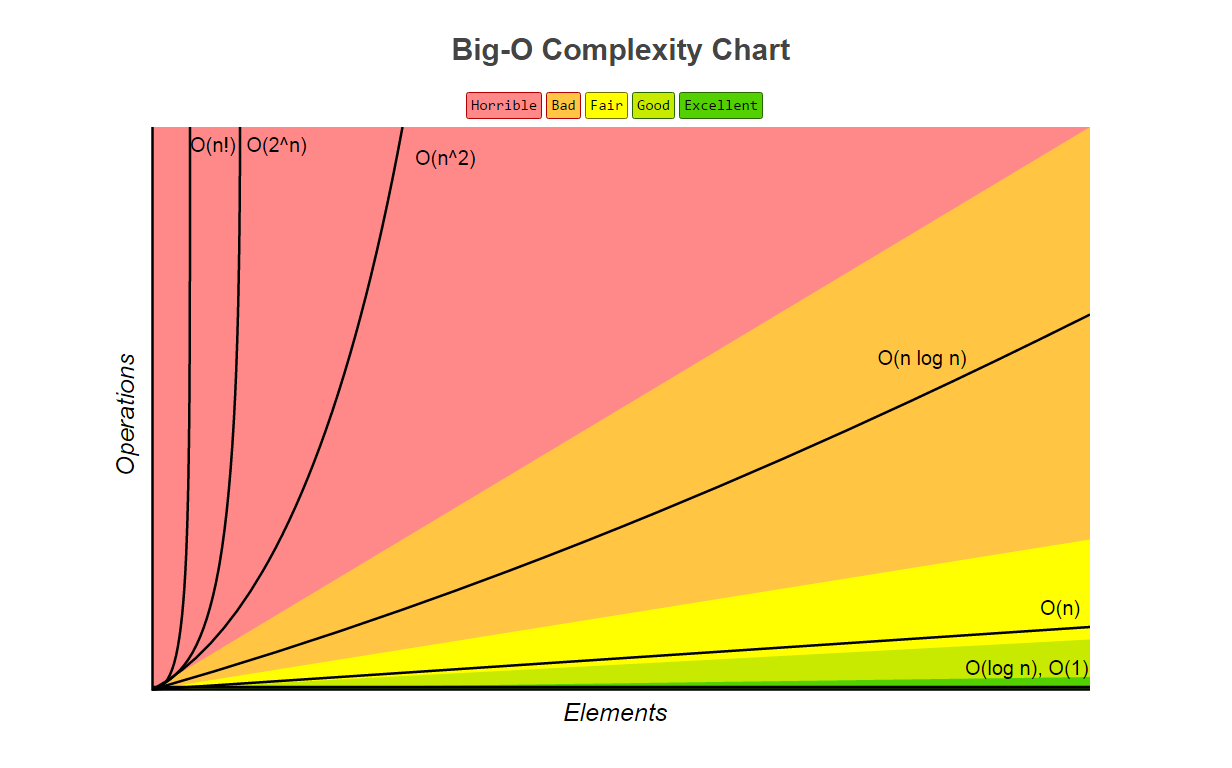
下面的两张图是常见的数据结构和算法的时间复杂度和空间复杂度。
本文主要阐述了算法的衡量标准,引入了Big O notation概念,重点解释了空间复杂度和时间复杂度求解方法和过程。
本文35%为翻译组合,65%为原创
http://bigocheatsheet.com/
https://www.cs.northwestern.edu/academics/courses/311/html/space-complexity.html
https://rob-bell.net/2009/06/a-beginners-guide-to-big-o-notation/
http://baike.baidu.com/link?url=MKCV_wcnPHwg_9fUksGf5qprZbSKaWeKkuuEd-IR_1mGjy6I7oFfttGlIG4Lgq9fHOSsd2wnp5Qa2K-EJe7N9IJrzhA0d_UzIXlTWeaehKrXwOYLNxp8uaBgn-LGISXs
http://blog.jobbole.com/55184/
http://baike.baidu.com/link?url=JR_8kNJ8W8BmTrs9lSvSF2rlsFVF5wYYTLhvvpot0SZcnPOYo-DF4L6TXklS05lDjCe46FVi2EaF3iqlO-m7vPu_X4bqerpJSQgQG10Xbok5Kt3xru_CIxZwdAVPzsn0xf_yqLlPv400J_iyQwgBjK
https://gradeup.co/space-and-time-complexity-i-c0b375f2-b5fc-11e5-867e-9b5bffc0cf23
http://btechsmartclass.com/DS/U1_T4.html
http://wenku.baidu.com/link?url=99i1IFK86QaNIGOD1tA4F3VQ5QbqkP0ARnRhLKeFdufoenzHjE10Nh7X1FJHMatFLpUuBzdBwtcYGvQFt7JCzKtuvEJ1g3Prwkc_E6Uf
http://btechsmartclass.com/DS/U1_T3.html
原文:http://www.cnblogs.com/ehcoo/p/6354588.html