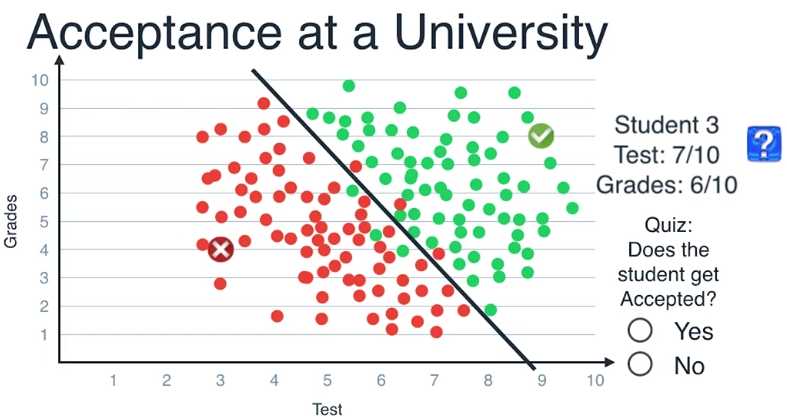
我们以这条线为模型,每当接到新的学生申请,我们把他们的成绩画在坐标图上
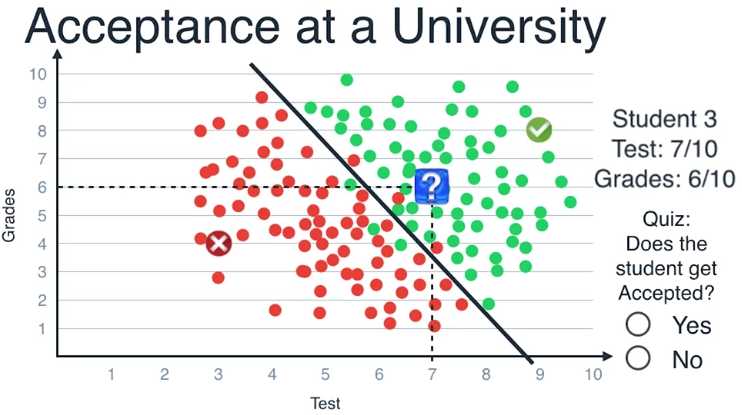
如果数据点是在这条线的上方,那么预测他们会被录取
如果数据点是在下方,则预测他们会被拒绝,学生的数据坐标为(7,6)
位于直线的上方,因此我们判断这个学生会被录取
这种方法叫做逻辑回归(Logistic Regression)
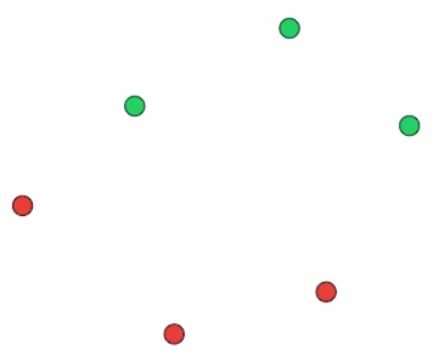
我们如何找到这条最好地分割数据点的线?,让我们看上图这个简单的例子
如何画出一条线以最好地区分绿色数据点和红色数据点
计算机无法依靠视觉来画出这条线,所以我们从画一条像这样的随机的线开始
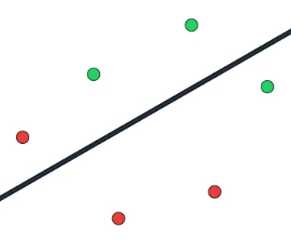
有了这条线,我们再随机地规定,位于线的上方的点为绿色,下方的点为红色
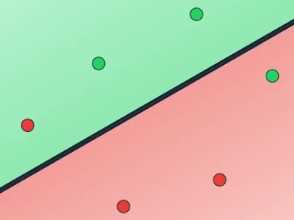
然后就像线性回归那样,我们先计算这条线的效果,一个简单的测量误差的标准是出错的数目
即被错误归类的数据点的数量,这条线错判了两个点,一个红色的点和一个绿色的点
因此我们说它有两个错误,仍然与线性回归类似,我们移动这条线
通过梯度下降算法(gradient descent)最小化错误数量
如果沿着这个方向稍微移动这条线,我们可以看到它开始能正确地归类其中一个数据点
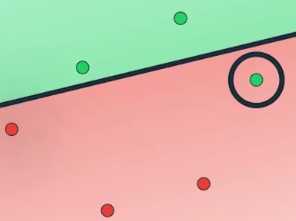
把错误数目降低到一个,如果继续移动这条线,它正确地归类了另一个点
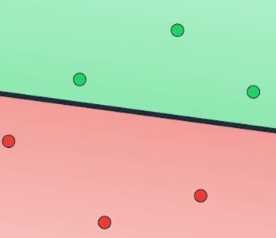
错误数目被降低到了零
实际使用中,为了正确地使用梯度下降算法,我们需要最小化的并不是错误数目
取而代之的是,能代表错误数目的对数损失函数(log loss function)

上图中有六个数据点,其中四个被正确分类,它们是两个红色和两个绿色
两个被错误归类,它们是一个红色和一个绿色
误差函数会对这两个被错误归类的数据点施加很大的惩罚,而对四个被正确归类的点施加很小的惩罚
在这门课中我们将会正式地学习误差函数公式
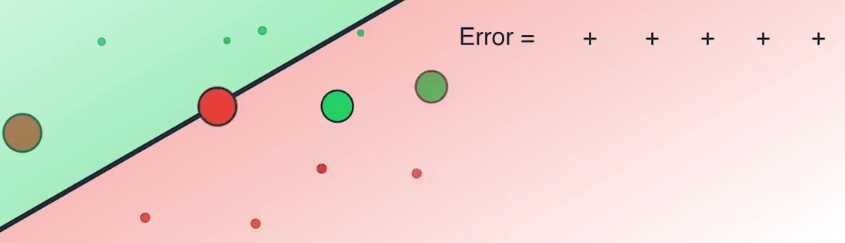
我们现在使用所有数据点的错误之和作为误差函数,我们得到了一个很大的误差值
因为两个被错判的点带来了很大的误差

如上图,现在四处移动这条线以将误差降到最小,如果我们沿着这个方向移动这条线
可以看到有些误差减小了,有些则微微增加了,但总体上,误差之和变小了
因为我们正确地归类了之前被错判的两个点
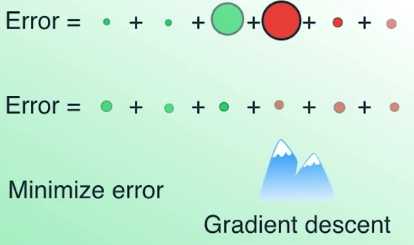
这个过程的意图是找出能最小化误差函数的最佳拟合线
我们如何最小化误差函数?依旧是使用梯度下降算法
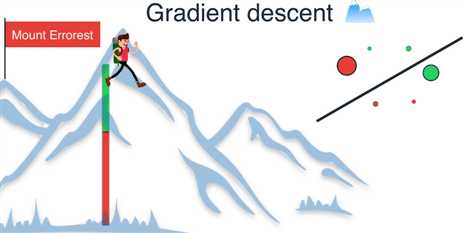
现在我们来到珠穆朗玛峰顶,我们所在的位置很高,因为此时有很大的误差
这可以从绿色和红色区域之和的大小中看出
我们探索四周寻找下降最大的方向 ,或者等价地寻找能通过移动直线最大程度减小误差的方向
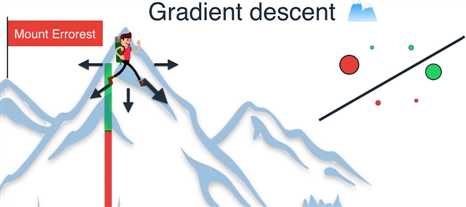
我们决定沿着这个方向前进一步,现在只有一个点被错误地归类
我们可以看到这种方法如何减小误差函数,把我们从山顶上带下来,
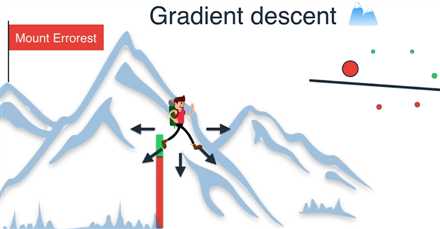
我们继续这样做,沿着最大程度减小误差的方向前进一步,就到达了山底
因为我们已经将误差减小到了最小值
【Deep Learning Nanodegree Foundation笔记】第 1 课:Logistic Regression
原文:http://www.cnblogs.com/custer/p/6357477.html