神经网络是一种受大脑工作原理启发的模式。 它在许多应用中广泛使用：当您的手机解释并理解您的语音命令时，很可能是神经网络正在帮助理解您的语音; 当您兑现支票时，自动读取数字的机器也使用神经网络。

Non-linear Classification 

 当输入数据特征过多，像上面的例子，当使用三次幂的特征时，可以超过170，000项，使我们的逻辑回归难以运行。

还有在计算机视觉中，图片的表示是通过像素矩阵表示的，如上图所示。那么假设一个图片是简单的50×50px，其特征数为2500（7500 if RGB），如果使用平方特征将达到百万级别，逻辑回归将无法适用。

Neurons and the brain

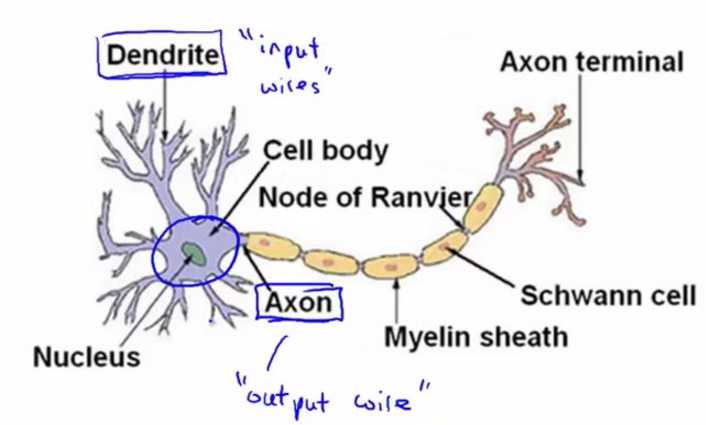
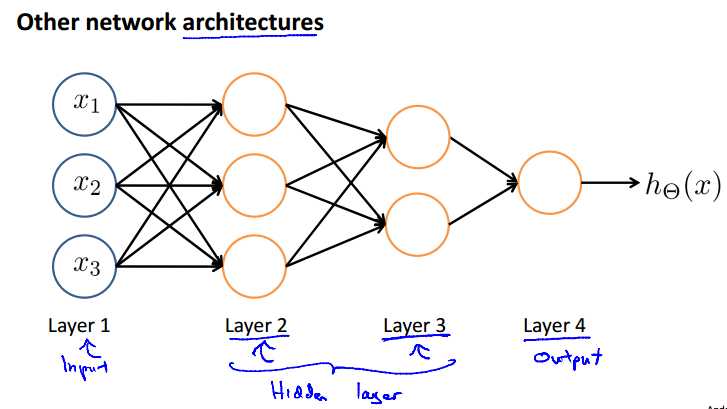
为模仿大脑的工作方式，神经网络可以类似的分为输入的数据特征，中间的数据处理层，和最后的输出。

Model Representation 

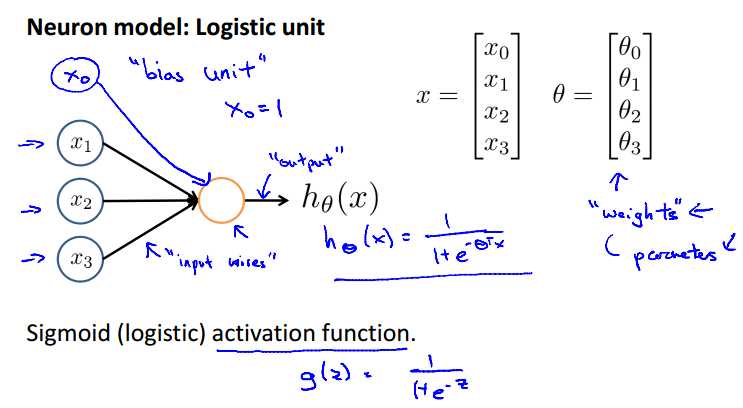
神经网络的简化形式如上图所示，x1，...xn为输入特征，输出为假设函数的结果。在模型中，通常会有一个额外的输入x0，我们称为"bias unit"（偏执单元），通常取值为1。

神经网络中我们依然使用逻辑回归中的逻辑函数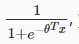，有时也称之为‘sigmoid (logistic) activation function‘。同时，那些参数theta也可以称为权值("weights")。

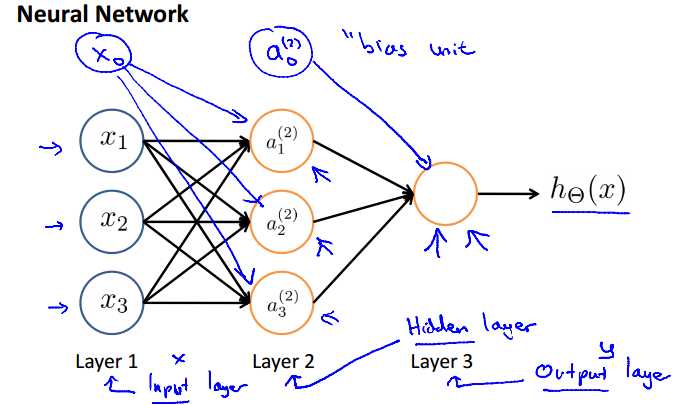
第一层为输入层（"input layer"），最后一层为输出层，输入层和输出层（"output layer"）之间的所有层统称为隐藏层（ "hidden" layer）。每一层的输入都可以增加一个偏执单元。

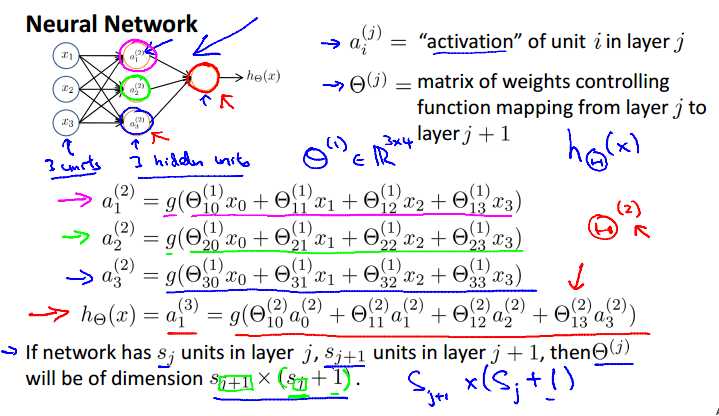
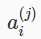=第j层的第i个激活结点（activation units.）

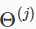=从第j层映射到j+1层的权重矩阵。

如果网络在第j层有Sj个单元（加上偏执单元），在j+1层有Sj+1个单元（不算偏执单元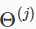），的维度将是。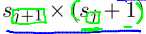

如上面的例子，theta1=3×4，theta2=1×4。

Forward propagation: Vectorized implementation 

为了将上面的神经网络的例子向量化，我们定义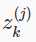表示逻辑函数g的参数。

例如第2层的第k个结点表示如下： 

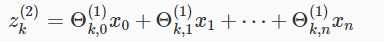
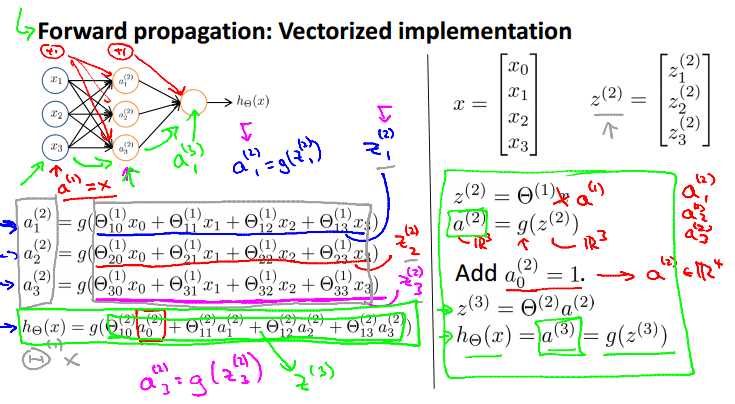
参数x和参数z向量化为：

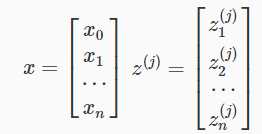
z和激活结点a可以表示为：

，

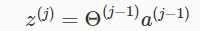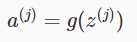
最后的输出为：

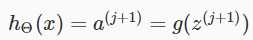
注意：请在每一层的输入加上偏执单元。

可以看出，我们在最后一步所做的和逻辑回归中其实是一样的。在网络中添加中间层目的是更好的处理复杂的非线性假设函数。

其实中间层数量可以是任意的，还有其他的网络结构。

Examples and Intuitions

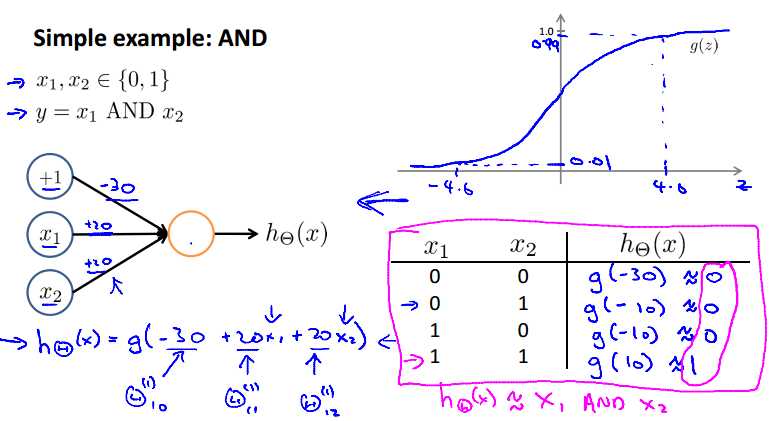
上面的例子实现了逻辑与。假设我们通过训练得到的theta={-30,20,20},将theta带入h（x）=g（-30+20x1+20x2），g（4.0）=0.99，g（-4.0）=0.01，由相应的函数值得到上面的真值表。

下面再给出一个例子实现逻辑或，训练得到的参数theta={-10,20,20}。

下面是一个更加复杂的例子，实现的是异或XNOR。

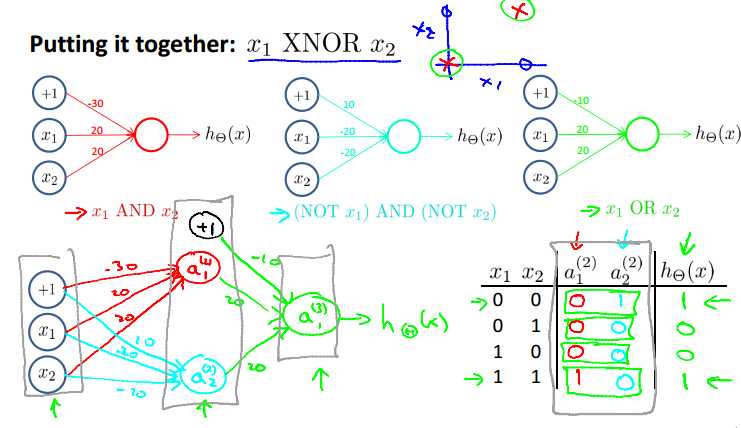
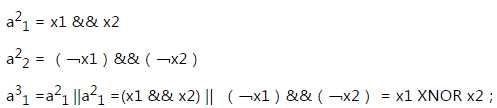
由上面的式子可得到上面的网络结构。

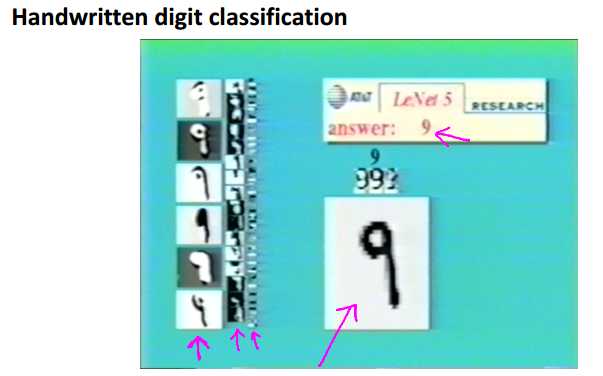
一个具体应用：手写数字识别。

Multiclass Classification

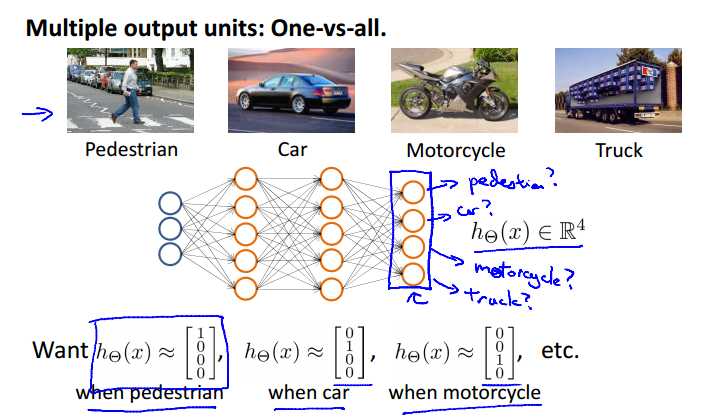
为了实现多元分类，需要假设函数返回一个向量值。如上面的例子，每个输出单元代表一个特定分类，每一个输出向量只有一个分量可以为1，值为1的分量代表特定的分类。

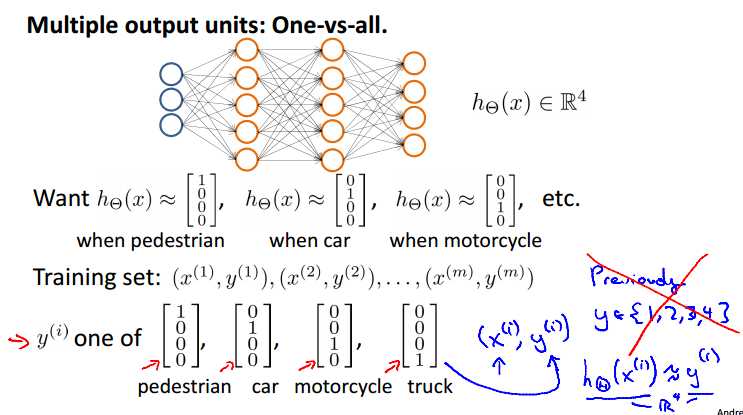
分类结果集合可以为：

网络最后形式为：

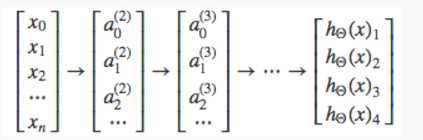
h（x）i表示第i类的预测函数。

参考：http://blog.csdn.net/abcjennifer/article/details/7749309

斯坦福机器学习视频笔记 Week4&Week5 Neural Networks

原文：http://www.cnblogs.com/yangmang/p/6359786.html