公式推导偷个懒,直接用别人的了
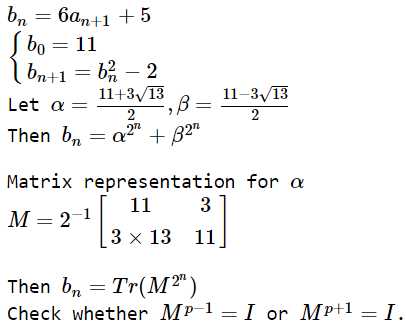
如果117是p的二次剩余,矩阵乘法部分,M的循环节就是p-1,否则是p+1。判断方法是勒让德符号,很好写,快速幂判断117的(p-1)/2次方是不是1.当然你也可以不判循环节,循环节取p^2-1,但是会慢。
python写的,本来做好了用c++重写的准备的,没想到居然过了。以前这种50000 cases的题py,pypy过不去

def loop(p): if pow(117,(p-1)>>1,p)==1: return p-1 return p+1 def b(n, p): i=(p+1)//2 T = [[11*i%p,3*i%p], [39*i%p,11*i%p]] n=pow(2,n,loop(p)) T = mat_pow(T, n, p) return (T[0][0]+T[1][1]) def mat_mult(A, B, p): C = [[0,0],[0,0]] for i in range(2): for j in range(2): for k in range(2): C[i][j] += A[i][k]*B[k][j] C[i][j] %= p return C def mat_pow(A, p, m): if p==0:return [[1,0],[0,1]] if p == 1: return A if p % 2: return mat_mult(A, mat_pow(A, p-1, m), m) X = mat_pow(A, p//2, m) return mat_mult(X, X, m) def a(n,p): return (b(n-1,p)-5)*pow(6,p-2,p)%p t=input() for i in range(t): n,p=map(int,raw_input().split()) if p==2 or p==3:print(1) else:print(a(n,p))
Project Euler 492的话数大一些,还要判一下素数,我用的miller_rabin,pypy跑了50s左右。miller_rabin的代码可以当模板用,51nod1186,1106都能用

import random from time import clock def loop(p): if pow(117,(p-1)>>1,p)==1: return p-1 return p+1 def b(n, p): i=pow(2,p-2,p) T = [[11*i,3*i], [39*i,11*i]] n=pow(2,n,loop(p)) T = mat_pow(T, n, p) return (T[0][0]+T[1][1]) def mat_mult(A, B, p): C = [[0,0],[0,0]] for i in range(2): for j in range(2): for k in range(2): C[i][j] += A[i][k]*B[k][j] C[i][j] %= p return C def mat_pow(A, p, m): if p==0:return [[1,0],[0,1]] if p == 1: return A if p % 2: return mat_mult(A, mat_pow(A, p-1, m), m) X = mat_pow(A, p//2, m) return mat_mult(X, X, m) def a(n,p): return (b(n-1,p)-5)*pow(6,p-2,p)%p def miller_rabin(n): if(n==1):return False d = n - 1 s = 0 while d % 2 == 0: d >>= 1 s += 1 for repeat in range(20): a = 0 while a == 0: a = random.randrange(n) if not miller_rabin_pass(a, s, d, n): return False return True def miller_rabin_pass(a, s, d, n): a_to_power = pow(a, d, n) if a_to_power == 1: return True for i in range(s-1): if a_to_power == n - 1: return True a_to_power = (a_to_power * a_to_power) % n return a_to_power == n - 1 def B(x,y,n): s=0 for i in range(x,x+y+1): if miller_rabin(i): s=s+a(n,i) return s start=clock() print(B(10**9,10**7,10**15)) print(clock()-start,‘seconds‘)
51nod 1361 有一种递推 Project Euler 492
原文:http://www.cnblogs.com/czp001/p/6361447.html