举个栗子。
我说我射击特别厉害,平均能打到8环,那么如何验证我是不是在吹牛逼呢,那就让我做几次射击看看我水平到底怎么样。
首先你选择相信我,假设我没吹牛,我的成绩在8环附近(这就是
原假设)。
我作为一个8环水平的选手,射中的环数应该服从一个平均值为8的高斯分布。
但是事先说好我的原则:
1、可能我当天没吃饱饭呀、或者心情不好呀,而且也就只让我射击几次,我可能发挥不好等等的,所以
你不能轻易怀疑我,如果我打7环、6环甚至4环你也不能怀疑我在吹牛;
2、但是毕竟作为一个8环水平的选手,基本功还应该是在的,如果我只打出了2环,你就会怀疑我是不是在吹牛了,请注意,
作为一个8环水平的选手,打出2环可是概率极低的事情!
那么根据这个规则我们设置一个阈值比如3.6环(这个阈值就是
临界值),如果我的成绩为2环(我的成绩是
观察值),那我就是在吹牛。注意作为一个8环选手,打出小于这个阈值的概率是极低的(这个概率就是
显著性水平)。
还有一种判断我是不是在吹牛的方法是,我已经打完了,计算打出小于我这个成绩的概率(这个概率是
p值),如果这个概率小于显著性水平,则说明我的成绩小于于临界值,则说明我在吹牛;反之则我没吹牛。(这个部分结合下面那个图来理解)
用统计的说法就是:
1、
不轻易拒绝原假设。原假设即使真的成立,而观察的样本由于数量较少,观察值存在一定的波动。所以我们要给原假设一定范围的容忍度,这个容忍度要尽可能大,观察值出现在这个范围内都是可以容忍的。
2、小概率事件发生不正常。如果小概率事件还是发生了,那么就说明原假设有问题。
结合这两点,我们设置一个随机变量的区域,这个区域是偏离原假设的,并且发生在这个区域的概率很小,如果实际观察到的值还是出现在这个不太可能出现的范围内,那么我们可以拒绝原假设。
两种决定是否接受原假设的方法:
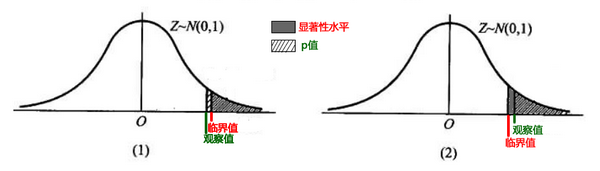
1、给定发生偏离原假设极端情况的概率(这就是显著性水平alpha),可以计算得到对应的临界值(参照图1,偏离原假设的阴影部分面积表示显著性水平,对应的坐标表示临界值)。若观察值在临界值范围内,表示出现这种现象都是比较正常的,则可接受原假设;若观察值超出临界值范围,则表示在原假设条件下出现了不太可能的现象,那么我们就怀疑原假设的成立性,则拒绝原假设。
2、给定发生偏离原假设极端情况的概率。计算出现观察值及比观察值还要偏离原假设的概率(这就是p值)。(参照下面这个图来理解)若p>alpha,则表示观察值在临界值范围内,则可接受原假设(如图1);若p<alpha,则表示观察值在临界值范围之外,则拒绝原假设(如图2)。p值是一个人工定义的东西,它其实还是通过判断观察值是否在临界值范围内来决定是否接受原假设。
总结下:
对于一个假设,我不知道它是否成立,而且实际测试过程中也存在许多非确定性因素可能导致我的测试过程不准确,那么我给出一个出现错误的容忍度(也就是显著性水平alpha),根据这个容忍度可以得到相应临界值(若观察值在这个范围内都是正常的,否则不正常),然后将观察值和这个值比较。
但是有些情况下观察值不太好看出来,我们可以计算出发生观察情况以及更坏情况的值(也就是p值)。若p值比alpha值大,则表明观察值在临界值范围内,可接受原假设(如图1);若p值比alpha值小,则表明观察值在临界值范围外,则决绝原假设(如图2)。
