一直以为背包这种东西除了pack就是bag，没想到竟然还有knapsack这种说法，嗯，大年初一，鸡年大吉，本来想把wiki上的东西理一下的，但是发现这东西排版实在是太蛋疼了……
背包问题，简单的说，是在背包内所装物品不超过其容量的情况下，所装的物品价值达到最大值，也就是说，在这种情况下，任何一个背包内物品和背包外物品兑换，在不超出背包容量的基础上，其兑换后的值不可能大于其原值。其最早在1897年被提出，啊刚好离今年120年呢……
到现在为止分为三种背包，0-1knapsack,bounded knapsack and unbounded knapsack。
0-1背包即：在
Given a set of n items numbered from 1 up to n, each with a weight wi and a value vi, along with a maximum weight capacity W
时，在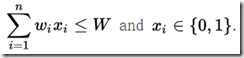
的限制下，需要找到
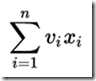的最大值，而其余两种背包更改xi的条件，使其变为：
bounded knapsack:
unbounded knapsack:
以上即是背包的说明。
然后是0-1背包的推理：
在网上看到一篇论文，里面关于01背包的子问题证明让我影响深刻：
如何证明01背包的解来源于其子问题？
假设{x0,x1,x2,x3,x4…xn}是一个01背包的最优解（x皆为0/1）那么，我们假设{x0,x1,x2,x3…xn-1}不是其子问题W=C-wn的最优解，那么一定存在另外的{y0,y1,y1,y2,y3…yn-1}(y=0||1）是该问题的最优解W=c-wn，那就存在{y0,y1,y2,y3…yn-1,xn}这样的序列，其价值大于{x0,x1,x2,x3,x4…xn}，这与给出调节相矛盾，所以假设不可能，所以结论是背包问题可以被拆成拾取物品的子问题
（即不是说W-1为W的子问题这种说法，也不是W-C是W的子问题，不同容量背包之间是否为子问题是由物品的重量决定的）
以下是例题：
The input consists of several test cases. Each test case begins with a real number C≤2000<?XML:NAMESPACE PREFIX = "[default] http://www.w3.org/1998/Math/MathML" NS = "http://www.w3.org/1998/Math/MathML" />C≤2000 giving the capacity of the knapsack, and an integer n≤2000n≤2000, giving the number of objects. Then follow nn lines, each giving the value and weight of the nn objects. Both values and weights will be integers between 11 and 1000010000.
For each test case, output a line containing the number of items chosen, followed by a line containing the indices of the chosen items (the first item has index 00, the second index 11, and so on). The indices can be given in any order.
Sample Input 1
Sample Output 1
5.3 3 1 5 10 5 100 5 6.1 4 5 4 4 3 3 2 2 1
1 2 3 1 2 3
code:
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
#define size_ 3000
#define math 1000
using namespace std;
struct item
{
int id=0;
int val=0;
int wei=0;
};
int dp[size_][size_] = { 0 };
int main(void)
{
double cap_t;
int ite;
while (scanf("%lf %d",&cap_t,&ite)!=EOF)
{
int cap = cap_t;
vector<item>sto(ite+1);
for (int i = 1; i <= ite; i++)
scanf("%d %d", &sto[i].val, &sto[i].wei),sto[i].id=i-1;
for (int i = 1; i <= ite; i++)
{
for (int j = 1; j <= cap; j++)
{
if (sto[i].wei > j)
{
dp[i][j] = dp[i - 1][j];
}
else
{
if (dp[i - 1][j - sto[i].wei] + sto[i].val > dp[i - 1][j])
{
dp[i][j] = dp[i - 1][j - sto[i].wei] + sto[i].val;
}
else
{
dp[i][j] = dp[i - 1][j];
}
}
}
}
int capp = cap;
vector<int>ans;
for (int i = ite; i >= 1&&capp>0; i--)
{
if(capp - sto[i].wei>=0)
if (dp[i][capp] == dp[i - 1][capp - sto[i].wei] + sto[i].val)
{
ans.push_back(i - 1);
capp -= sto[i].wei;
}
}
int flag = 0;
cout << ans.size() << endl;
for (int i = 0; i < ans.size(); i++)
{
if (flag)
cout << " " << ans[i];
else
{
cout << ans[i];
flag = 1;
}
}
cout << endl;
}
}
knapsack problem（kattis-knapsack）
原文：http://www.cnblogs.com/stultus/p/6354209.html