题目链接 https://www.luogu.org/problem/show?pid=3371
题目:
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入格式:
第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
输出格式:
一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
0 2 4 3
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=15
对于40%的数据:N<=100,M<=10000
对于70%的数据:N<=1000,M<=100000
对于100%的数据:N<=10000,M<=500000
样例说明:
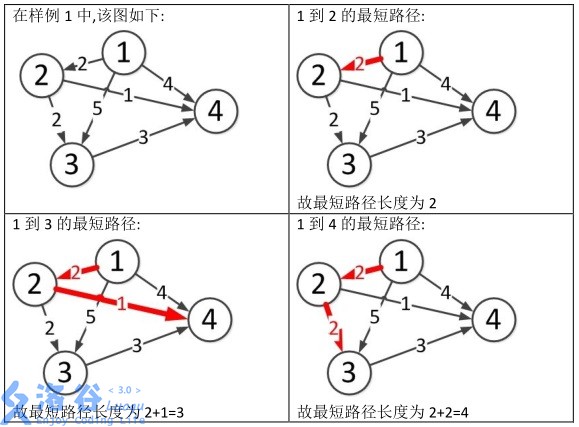
分析:
单源最短路,看了看数据N<=10000,M<=500000用bellman——ford会超时,单纯的用dijkstra也要超时,先讲一下dijkstra算法的思想;dijkstra算法包括两个步骤:1找到最短距离已经确定的点。2从这个点出发确定相邻的点的最短距离。在最开始只有s——s的最短路径是确定的,所以先从s开始,那么如果模拟出来,定义d[i]表示从s到i号顶点的最短距离。
代码:
#include<cstdio> #include<iostream> #define ll long long #define INF 2147483647 using namespace std; int n,m,s; ll cost[10010][10010]; ll d[10010]; bool used[10010]; void dijkstra(int s){ fill(d,d+n+1,INF); fill(used,used+n+1,false); d[s]=0; while(1){ int v=-1; for(int u=1;u<=n;u++) if(!used[u]&&(v==-1||d[u]<d[v])) v=u; if(v==-1) break; used[v]=true; for(int u=1;u<=n;u++) d[u]=min(d[u],d[v]+cost[v][u]); } } int main(){ for(int i=0;i<=10001;i++) for(int j=0;j<=10001;j++) cost[i][j]=INF; cin>>n>>m>>s; for(int i=1;i<=m;i++){ int u,v,w; scanf("%d%d%d",&u,&v,&w); cost[u][v]=w; } dijkstra(s); for(int i=1;i<=n;i++) printf("%lld ",d[i]); cout<<endl; return 0; }
这个程序复杂度是v*v的很明显对于题目中的数据范围要超时的,想想怎么优化,取出最小值。。。。想到什么了,小顶堆,对,可以用小顶堆维护最短路径,用邻接表来维护边,那么复杂度就变成了ElogV,下面是代码,简单易懂;
优化版
#include<cstdio> #include<cstring> #include<iostream> #include<queue> #include<vector> #include<algorithm> #define ll long long #define INF 2147483647 using namespace std; int n,m,s,head[50010],ecnt; ll d[10010]; bool used[10010]; struct edge{ int to,next,w; }es[500010]; void addedge(int u,int v,int w){ es[ecnt].to=v; es[ecnt].next=head[u]; es[ecnt].w=w; head[u]=ecnt++; }//邻接表存边。 typedef pair<int,int> P;//用于存到达点的最短路径 void dijkstra(int s){ priority_queue<P,vector<P>,greater<P> > q;//按照P第一个元素从小到大取出的队列 fill(d,d+n+1,INF); fill(used,used+n+1,false); d[s]=0; q.push(P(0,s)); while(!q.empty()){ P p=q.top();q.pop(); int u=p.second; if(used[u]) continue; used[u]=true; int pp=head[u]; while(pp!=-1){ int v=es[pp].to; if(!used[v]&&d[v]>d[u]+es[pp].w){ d[v]=d[u]+es[pp].w; q.push(P(d[v],v)); } pp=es[pp].next; } } } int main(){ memset(head,-1,sizeof(head)); cin>>n>>m>>s; for(int i=1;i<=m;i++){ int u,v,w; scanf("%d%d%d",&u,&v,&w); addedge(u,v,w); } dijkstra(s); for(int i=1;i<=n;i++) printf("%lld ",d[i]); putchar(‘\n‘); return 0; }
总结:没什么总结的,这个是dijkstra算法的模板。
dijkstra算法详讲 洛谷P3371 【模板】单源最短路径
原文:http://www.cnblogs.com/zzozz/p/6378526.html