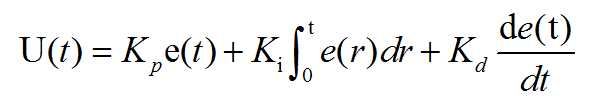
先解释一下公式中的几个量
变量t只是表示这些都是时域函数而已(r,dr只是中间变量,积分结果还是关于t的函数)
U(t)表示当前控制器的输出量
e(t)表示当前控制器的输入量(一般为设定量与当前量的差值delta=Uset-Unow)
PID,其实对应的是三个量
Proportion(比例),记量Kp
Integration(积分),计量Ki
Differential(微分),记量Kd
那么如何理解这个公式呢?
首先假设对于一个需要调节的系统来说,为了方便说明,我们以热水器为例,我们当前的目标是将水温从80度升至90度并稳定
1.Kp是最基础的比例系数,让温度差成比例放大为电热丝的发热量是一个很显然的思路,越接近目标越要慢慢来嘛
2.Ki是对应积分的系数,引入这个量是为了解决系统存在静差的问题,比如当升至89度时,实际上电热丝的发热量已经很少了,可能刚好只能抵消水的散热量,如果我们什么都不做,水温将稳定在89度,这仍与我们想要的稳态有差异。
所以我们引入一个时间的积分,来让电热丝发热量在一段时间以后增加,使水温继续上升
3.Kd是对应微分的系数,引入这个量是为了防止系统出现超调现象,比如水温明明已经达到了90度,但电热丝温度还很高,所以水温还会继续上升。正确的做法是在接近90度时进一步减少发热量,用电热丝的余温让水温达到90度
这个公式的实现是有两种形式的:位置式和增量式
首先说明一下,在实际应用中,时间只能细分到有限的单位监测时间T,因此我们把第k次检测当做时间
位置式![]()
位置式是遵从原公式的,因此不难由原公式得到
但注意此处的Ki‘ , Kd‘ 不是原来的Ki , Kd了
Ki‘=Ki*T (粗略的定积分)
Kd‘=Kd/T (粗略的微分)
但是观察一下位置式所需要的量,我们发现积分处的求和所需要的运算量也忒大了,有没有方法简化?引入增量式
增量式![]()
只是用位置式相邻两项作差,却相当于把一个O(N)级别的求和问题变成了一个简单的二阶递推,棒棒哒
这利用了我们需要对每一个时刻的U(k)进行求解的特性,之前的结果是可以利用的,因此没有必要重复求和
整理一下二阶递推
递推式![]()
To be continue...
待加入,三个量的整定
原文:http://www.cnblogs.com/KningTG/p/6385786.html