https://vjudge.net/problem/UVA-1151
题意:
平面上有n个点,你的任务是让所有n个点连通。为此,你可以新建一些边,费用等于两个端点的距离平方和。另外还有q个套餐可以购买,如果你购买了第i个套餐,该套餐中的所有结点都变得相互连通,第i个套餐的花费为Ci。
思路:
这道题比较容易超时。可能需要用到并查集的路径压缩,我下面的代码就是用了路径压缩,不然要超时。也是看了别人的代码才知道还有这种省时间的做法。
先介绍一下路径压缩吧:
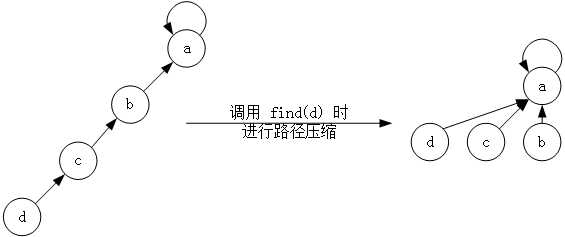
如果并查集像一字长蛇这样排列的话,寻找起来就比较费时间,但如果像图2一样的话,一下子就可以找到根了。压缩的方法也是挺简单的。
1 int r = x; 2 while (r != p[r]) r = p[r]; 3 int i = x, j; 4 while (p[i] != r) 5 { 6 j = p[i]; 7 p[i] = r; 8 i = j; 9 }
题目的做法就像紫书上说的那样,先不考虑套餐算一遍,然后枚举套餐的方法,这里的话二进制枚举法非常方便。
1 #include<iostream> 2 #include<cstring> 3 #include<algorithm> 4 #include<vector> 5 using namespace std; 6 7 const int maxn = 1000 + 5; 8 9 int n, m, q, cnt; 10 int p[maxn]; 11 vector<int> g[10]; //方案集合 12 int c[10]; //方案价格 13 14 //边 15 struct node 16 { 17 int u; 18 int v; 19 int dist; 20 }edge[maxn*maxn]; 21 22 //点 23 struct node2 24 { 25 int x, y; 26 }a[maxn]; 27 28 int find(int x) 29 { 30 //return p[x] == x ? x : find(p[x]); 用这个会超时 31 //路径压缩 32 int r = x; 33 while (r != p[r]) r = p[r]; 34 int i = x, j; 35 while (p[i] != r) 36 { 37 j = p[i]; 38 p[i] = r; 39 i = j; 40 } 41 return r; 42 } 43 44 bool cmp(node a, node b) 45 { 46 return a.dist < b.dist; 47 } 48 49 //计算距离平方和 50 int cacl_dist(node2 a, node2 b) 51 { 52 return (a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y); 53 } 54 55 void init() 56 { 57 for (int k = 1; k <= n; k++) p[k] = k; 58 } 59 60 int Kruskal() 61 { 62 int num = 0; 63 int ans = 0; 64 for (int i = 0; i < cnt ; i++) 65 { 66 int x = find(edge[i].u); 67 int y = find(edge[i].v); 68 if (x != y) 69 { 70 p[x] = y; 71 ans += edge[i].dist; 72 num++; 73 } 74 if (num == n - 1) return ans; 75 } 76 return ans; 77 } 78 79 80 void solve() 81 { 82 init(); 83 int ans = Kruskal(); 84 //二进制枚举方案 85 for (int i = 0; i < (1 << q); i++) 86 { 87 init(); 88 int cost = 0; 89 for (int j = 0; j < q; j++) 90 { 91 if (i & (1 << j)) 92 { 93 cost += c[j]; 94 int x = find(g[j][0]); 95 for (int k = 1; k < g[j].size(); k++) 96 { 97 int y = find(g[j][k]); 98 if (x != y) 99 p[y] = x; 100 } 101 } 102 } 103 ans = min(cost + Kruskal(), ans); 104 } 105 printf("%d\n", ans); 106 } 107 108 int main() 109 { 110 //freopen("D:\\txt.txt", "r", stdin); 111 int T, t, s, kase=0; 112 scanf("%d", &T); 113 while (T--) 114 { 115 if (++kase > 1) printf("\n"); 116 scanf("%d%d", &n, &q); 117 118 //存储方案 119 for (int i = 0; i < q; i++) 120 { 121 g[i].clear(); 122 scanf("%d", &t); 123 scanf("%d", &c[i]); 124 for (int j = 0; j < t; j++) 125 { 126 scanf("%d", &s); 127 g[i].push_back(s); 128 } 129 } 130 131 for (int i = 1; i <= n; i++) 132 scanf("%d%d", &a[i].x, &a[i].y); 133 134 //存储边 135 cnt = 0; 136 for (int i = 1; i <= n;i++) 137 for (int j = i + 1; j <= n; j++) 138 { 139 edge[cnt].u = i; 140 edge[cnt].v = j; 141 edge[cnt].dist = cacl_dist(a[i], a[j]); 142 cnt++; 143 } 144 sort(edge, edge + cnt, cmp); 145 solve(); 146 } 147 return 0; 148 }
原文:http://www.cnblogs.com/zyb993963526/p/6388131.html