题目链接:https://uva.onlinejudge.org/external/118/11806.pdf
题意:
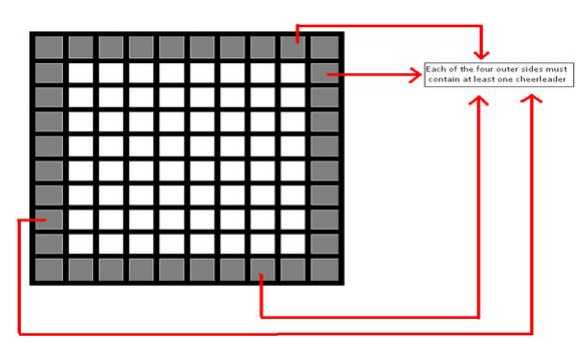
n行m列的矩阵上放k个棋子,其中要求第一行,最后一行,第一列,最后一列必须要有。有多少种放法;
分析:
要是没有那个条件,就直接是C(n*m,k)了,其实也可以转换过来。
设满足“第一行没有棋子”的方案数为A,“最后一行没有棋子”的方案数B,C,D;
然后用容斥原理可以求出。
这里用二进制表示这16种组合;满足偶数个条件为+;
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 const int MOD = 1000007; 6 const int maxn = 500; 7 int C[maxn+10][maxn+10]; 8 9 int main() 10 { 11 memset(C,0,sizeof(C)); 12 C[0][0] = 1; 13 14 for(int i=0;i<=maxn;i++) { 15 C[i][0] = C[i][i] = 1; 16 for(int j=1;j<i;j++) 17 C[i][j] = (C[i-1][j]+C[i-1][j-1])%MOD; 18 } 19 20 int t; 21 cin>>t; 22 int kase = 1; 23 while(t--) { 24 int n,m,k,sum = 0; 25 cin>>n>>m>>k; 26 for(int S=0;S<16;S++) { 27 int b = 0; 28 int r = n; 29 int c = m; 30 if(S&1) {r--;b++;} 31 if(S&2) {r--;b++;} 32 if(S&4) {c--;b++;} 33 if(S&8) {c--;b++;} 34 if(b&1) sum = (sum + MOD - C[r*c][k]) % MOD; 35 else sum = (sum + C[r*c][k])%MOD; 36 } 37 printf("Case %d: %d\n",kase++,sum); 38 } 39 40 return 0; 41 }
原文:http://www.cnblogs.com/TreeDream/p/6388054.html