对博弈树的理解 简单而言就是对每一步可能的结果进行分析 之后对当前步骤的下一步的所有可能结果进行分析而创建的树
专业表示极大极小博弈树:极大极小博弈树是因描绘这种结构的一种简单算法而得名。我们来对ttt游戏的结果分配一下分值。如果叉(X)获胜,则分值为1。如果圈(O)获胜,则分值为-1。现在,叉将试图获得最大化的分值,而圈将试图最小化分值。于是,第一位研究此问题的研究者决定把游戏者叉命名为max,并且把游戏者圈命名为min。因此,这个完整的数据结构就被命名为极大(Max)极小(Min)博弈树。
例如:
对于博弈树的创立过程需要对于任意种可能结果设定权重:例如黑白棋中设立以下几种权重
连三 100分
双连二 50分
平局 0分
不分胜负 1
其中如果评分时不分胜负则还会继续搜索,直到找到其他三种状态、
利用博弈树时,由于结果可能很多 所以需要进行必要剪枝,算法思路如下:
min电脑AI下棋时,如果考虑步数为0,则代表直接返回当前棋盘估值w(值越大代表对max越有优势,越小则代表对min越有优势,w=maxW-minW)。
如果考虑步数为N,先获取min电脑可以下棋的位置steps。
对于可以下棋的一步step,电脑AI下棋到step的第row行,第column列。
如果这时候min电脑已经赢了,则把棋盘回退一步,返回棋盘估值和下棋位置,不用再考虑其他走法了。
否则,min需要在每一种走法里面,选择一种走法,令max人类走N-1步之后,自己的优势保持最大(即w值最小)。
什么是alpha-beta剪枝呢?就是如果max人类当前一种走法1至少可以获取alpha优势,而另一种走法2,min电脑的一步棋则可能让人类获取比alpha更小的优势,那么max人类肯定不会选择走法2,所以计算在计算min电脑的走法时,min电脑的其他走法就不用再计算了。
最后min电脑经过steps.length种走法对比之后,选择w值最小的一种走法,把棋盘回退一步,并返回棋盘估值和下棋位置。
max走法类似,人类会选择w值最大的走法下棋,所以max函数和min函数分别代表人和AI下棋,互相递归调用,直到递归到步数为0时返回N步之后的估值。
如果一棵树博弈树的每个内部结点的第一个子结点都返回最优的解,那么称这棵树是良序的.对一个良序的博弈树,Alpha-Beta算法会修剪一些无必要搜索的子树,修剪之后的树就称为最小树(minimal tree,或者critical tree).当博弈树是良序的时候,Alpha-Beta算法所需要搜索子树都包含在这个最小树中.按照上述结点的分类方法,最小树中的所有结点的类型都是已定的,因为那些类型为undefined的结点都会被剪枝.
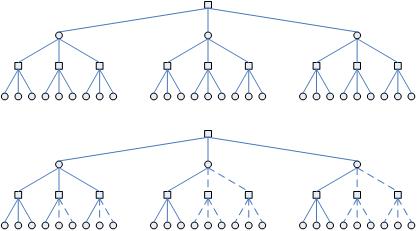
均匀博弈树及其最小树
如果一个博弈树的所有内部结点(interior
node)具有相同的分支因子,且所有的根结点到叶结点的深度相同,那么该搜索树就是一个均匀的(uniform).对于一个深度为d的均匀良序博弈树的的最小树,从根结点到叶结点,经历了d个边.设第i个边是其父结点的第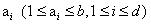 个分支.将所有
个分支.将所有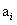 按照“.”连接起来形成一个串:
按照“.”连接起来形成一个串: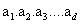 .设
.设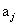 为该串中第一个大于1的值.如果不存在
为该串中第一个大于1的值.如果不存在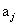 ,即所有的
,即所有的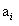 都为1,则该叶结点为PV结点.如果
都为1,则该叶结点为PV结点.如果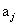 存在,那么
存在,那么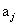 对应边的子结点一定为CUT结点.这时如果d
- j是偶数,那么该串对应的叶结点为CUT结点,否则,如果d - j是奇数,该叶结点为ALL结点.
对应边的子结点一定为CUT结点.这时如果d
- j是偶数,那么该串对应的叶结点为CUT结点,否则,如果d - j是奇数,该叶结点为ALL结点.
对一个CUT类型的叶结点,它对应的串存在着性质:对所有i,如果d - j是偶数,则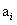 为1.这种串(除了全1的串)和CUT叶结点一一对应.这种串的个数为
为1.这种串(除了全1的串)和CUT叶结点一一对应.这种串的个数为 ,故此CUT叶结点的个数也为
,故此CUT叶结点的个数也为 .
.
同样,对一个ALL类型的叶结点,它对应的串存在着性质:对所有i,如果d - j是奇数,那么为1.这样的串(除了全1的串)和ALL叶结点一一对应.这样的串的个数为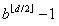 ,所以ALL叶结点的个数为
,所以ALL叶结点的个数为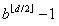 .再加上PV叶结点,一个最小树包含的叶结点个数为
.再加上PV叶结点,一个最小树包含的叶结点个数为 ,这也是在均匀博弈树中Alpha-Beta算法搜需要搜索的最少叶结点个数.
,这也是在均匀博弈树中Alpha-Beta算法搜需要搜索的最少叶结点个数.
参考博弈树建立代码。
int gameState(char _board[9]) { int state; static int table[][3] = { {0, 1, 2}, {3, 4, 5}, {6, 7, 8}, {0, 3, 6}, {1, 4, 7}, {2, 5, 8}, {0, 4, 8}, {2, 4, 6}, }; char chess = _board[0]; for (char i = 1; i < 9; ++i) { chess &= _board[i]; } bool isFull = 0 != chess; bool isFind = false; for (int i = 0; i < sizeof(table) / sizeof(int[3]); ++i) { chess = _board[table[i][0]]; int j; for (j = 1; j < 3; ++j) if (_board[table[i][j]] != chess) break; if (chess != empty && j == 3) { isFind = true; break; } } if (isFind) //got win or lose state = chess == o ? WIN : LOSE; else { if (isFull) //all position has been set without win or lose return DRAW; else { //finds[0] -> ‘o‘, finds[1] -> ‘x‘ int finds[2] = {0, }; for (int i = 0; i < sizeof(table) / sizeof(int[3]); ++i) { bool findEmpty = false; chess = 0xff; int j; for (j = 0; j < 3; ++j) if (_board[table[i][j]] == empty && !findEmpty) findEmpty = true; else chess &= _board[table[i][j]]; if ((chess == o || chess == x) && findEmpty) { isFind = true; if (o == chess) ++finds[0]; else ++finds[1]; } } if (finds[0] > 1 && finds[1] < 1) //2 ‘o‘ has been founded twice in row, column or diagonal direction state = -(INFINITY / 2) * finds[0]; else if (finds[1] > 1 && finds[0] < 1) //2 ‘x‘ has been founded twice in row, column or diagonal direction state = INFINITY / 2 * finds[1]; else //need to search more. state = INPROGRESS; } } return state; }
原文:http://www.cnblogs.com/KID-XiaoYuan/p/6392209.html