摘要：
1.信息的度量
2.信息不确定性的度量
内容：
1.信息的度量
直接给出公式
，这里的N(x)是随机变量X的取值个数，至于为什么这么表示可以考虑以下两个事实：
（1）两个独立事件X,Y的联合概率是可乘的，即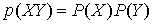
，而X,Y同时发生的信息量应该是可加的，即
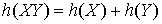，因此对概率取了负对数（保证非负）
（2）一个时间发生的概率越大，其信息量越小，因此对概率取了负对数（保证非负）
举两个例子便于理解：
一本50w字的史记的信息量是-ln(1/50w),2010年世界杯32支队伍谁会夺冠的信息量是-ln(1/32);注意：这里的ln是以2为底的，信息的单位是bit，并且都是假定概率分布都是均匀分布的
总结：直观理解其实就是给信息编码的过程，比如数字0-9的二进制表示只要ln10
2.信息不确定性的度量
直接给出公式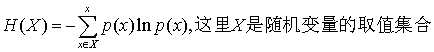
，也就是信息量的期望；这个值叫做熵
以下讨论几个分布：
对于最简单的0-1分布，假设p(x=1)=p,则p(x=0)=1-p，计算信息熵：
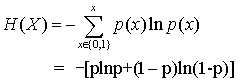
对于均匀分布，假设p(x=n)=1/N,其中N是随机变量的取值个数，计算信息熵：
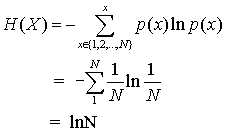
不加证明的给出结论：随机变量为定值时，熵最小；随机变量为均匀分布时，熵最大
讨论下二元随机变量的情况，为了直观解释和记忆，先给出如下图解：
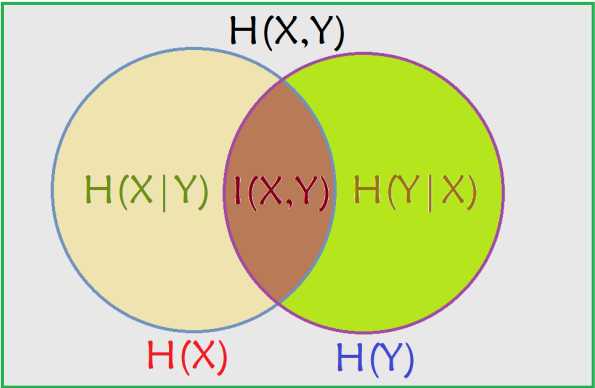
先说联合熵的定义，代表X,Y同时发生的不确定性；公式为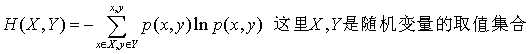
，从上图中理解就是两个大圆的面积。
再说条件熵，代表在已知一个变量发生的条件下，另一个变量发生所新增的不确定性；公式为：
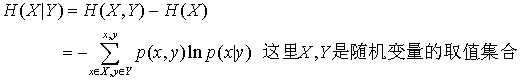，有兴趣的朋友可以自己推导一下是如何从（1）式到（2）式的，从上图中理解就是两个大圆去掉其中一个大圆所剩下的面积。
最后定义互信息（ID3算法中也叫信息增益），待续
原文：http://www.cnblogs.com/arachis/p/entropy.html