斐波那契(fib.pas/c/cpp)
题目大意
众所周知,斐波那契数列就是 F(n)=F(n-1)+F(n-2),F(1)=F(2)=1,然后大小为 n 的一维
斐波那契表就是 F(1),F(2),F(3),F(4)…F(n)。我们定义二维的斐波那契表的第(i,j)个位置也就是
a(i,j)=F(i+j-1),大小为 n 的二维斐波那契表如下表:
F(1) F(2) F(3) … F(n)
F(2) F(3) F(4) … F(n+1)
F(3) F(4) F(5) … F(n+2)
… … … … …
F(n) F(n+2) F(n+3) … F(2n-1)
我们定义k维大小为n的斐波那契表的第(i 1 ,i 2 ,…,i k )项a(i 1 ,i 2 ,…,i k )=F(i 1 +i 2 +…+i k -k+1)。 其中,
i 1 ,i 2 ,…,i k 均为不超过 n 的正整数。你的任务是,给你 n 和 k 要求求出 k 维大小为 n 的斐波那
契表所有元素之和 mod 1,000,000,007 的值。
输入文件
输入文件为 fib.in。
一行两个数 n 和 k。
输出文件
输出文件为 fib.out。
一行一个数表示答案
样例输入 1
2 2
样例输出 1
5
样例输入 2
4 1
样例输出 2
7
样例输入 3
1 3
样例输出 3
1
数据规模与约定
对于 20%的数据,n,k ≤10 5 ;
另有 20%的数据,k=1;
对于 60%的数据,k≤10^5
对于 100%的数据,n,k≤10^9+7
——————————————————————————题解
这是一个需要推两个矩阵的题
一个矩阵是在第k维里层和层之间的转移,一个矩阵是第k维到第k+1维
F[i][j]表示第i维第j层的和
S[i][j]表示第i维前j层的和

举个栗子n=4
1维时 1 1 2 3
n+1 1 1 2 3 5
2维的第一层
1 1 2 3
第二层
[1 2 3 4]+[1 1 2 3 5]-[1]
1 2 3 5
第二层的一二层
1 1 2 3
1 2 3 5
然后写矩阵
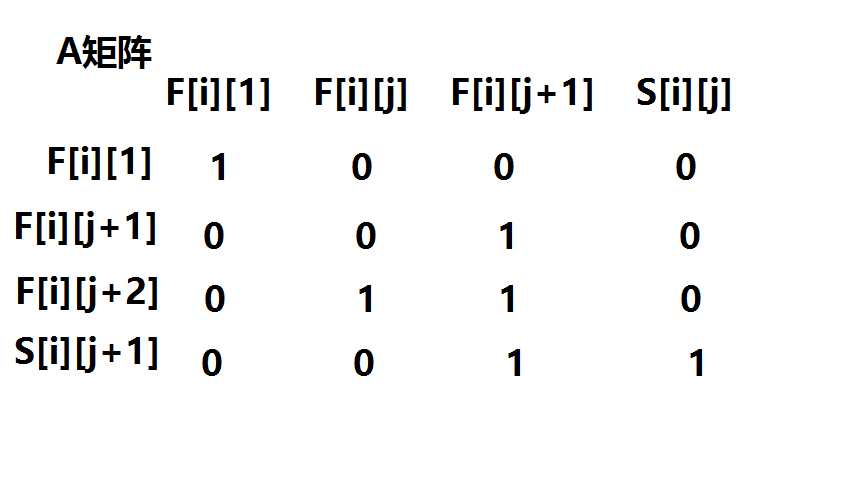
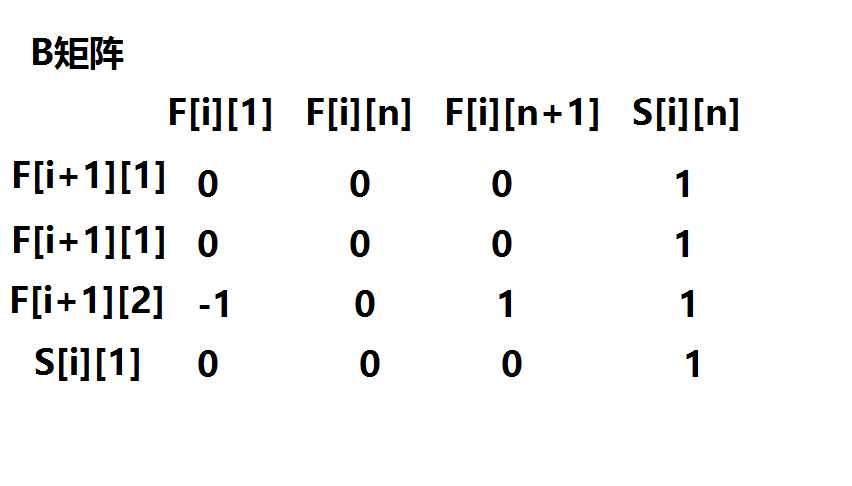
答案是A^(n-1)*B
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring>//important 4 #include <algorithm> 5 #define siji(i,x,y) for(int i=(x);i<=(y);++i) 6 #define gongzi(j,x,y) for(int j=(x);j>=(y);--j) 7 #define xiaosiji(i,x,y) for(int i=(x);i<(y);++i) 8 #define sigongzi(j,x,y) for(int j=(x);j>(y);--j) 9 #define ivorysi 10 #define inf 0x7f7f7f7f 11 #define mod 1000000007 12 typedef long long ll; 13 using namespace std; 14 struct node { 15 ll m[5][5]; 16 node() {memset(m,0,sizeof(m));} 17 node operator * (const node &rhs) const{ 18 node tmp; 19 siji(i,1,4) { 20 siji(j,1,4) { 21 siji(k,1,4) { 22 tmp.m[j][i]=(m[k][i]*rhs.m[j][k]+tmp.m[j][i])%mod; 23 } 24 25 } 26 } 27 return tmp; 28 } 29 }; 30 node pow(node c,int o) { 31 if(o==1) return c; 32 node t=pow(c,o>>1); 33 if(o&1) { 34 return t*t*c; 35 } 36 else { 37 return t*t; 38 } 39 } 40 int n,k; 41 void solve() { 42 scanf("%d%d",&n,&k); 43 if(n==1) {puts("1");return;} 44 node a,b,x; 45 ll u[5][5]={ {0,0,0,0,0},{0,1,0,0,0},{0,0,0,1,0},{0,0,1,1,0},{0,0,0,1,1} }; 46 memcpy(a.m,u,sizeof(u)); 47 ll z[5][5]={ {0,0,0,0,0},{0,0,0,0,1},{0,0,0,0,1},{0,-1,0,1,1},{0,0,0,0,1} }; 48 memcpy(b.m,z,sizeof(z)); 49 x=a; 50 x=pow(x,n-1); 51 x=x*b; 52 x=pow(x,k); 53 54 printf("%d\n",(ll)(x.m[4][1]+x.m[4][2]+x.m[4][3]+x.m[4][4])%mod); 55 } 56 int main(int argc, char const *argv[]) 57 { 58 #ifdef ivorysi 59 freopen("fib.in","r",stdin); 60 freopen("fib.out","w",stdout); 61 #else 62 freopen("f1.in","r",stdin); 63 #endif 64 solve(); 65 return 0; 66 }
原文:http://www.cnblogs.com/ivorysi/p/6395691.html