
(1,99,2)
(5,68,1)
(3,70,3)
(7,45,null)
主键不重复 不为空, 外键是另一个表的主键,必须能够给找到, 可以重复 可以空!
宏定义
模板
内联函数
递归
总之 模板会造成代码膨胀
cout<<typeid(d).name()<<endl; cout<<typeid(double).name()<<endl;
typeid可提供运行时信息,name函数打印出类型的首字母
int *a=new int(12); //..... free(a);
int *ip=static_cast<int*>(malloc(sizeof(int))); *ip=10; //..... delete ip;
double *a=new double[1]; //.... delete a;
D
int *ip=new int(12); for(int i=0;i<12;++i){ ip[i]=i; } delete []ip;
这里注意D答案,小心被骗, int(12)是初始化了一个值为12的int整型。int[12]是初始化了12个变量的数组
ESTABLISHED->CLOSE_WAIT->TIME_WAIT->CLOSED
ESTABLISHED->TIME_WAIT->CLOSE_WAIT->CLOSED
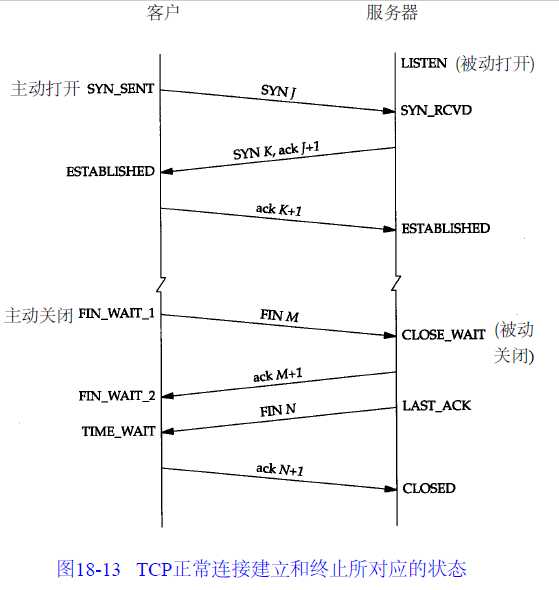
ESTABLISHED->FIN_WAIT_1->FIN_WAIT_2->TIME_WAIT->CLOSED
ESTABLISHED->FIN_WAIT_1->TIME_WAIT->CLOSED
IP
ICMP
ARP 已知ip地址求mac地址
RARP 已知mac地址求ip地址
epoll和select都是I/O多路复用的技术,都可以实现同时监听多个I/O事件的状态
epoll相比select效率更高,主要是基于其操作系统支持的I/O事件通知机制,而select是基于轮询机制
epoll支持水平触发和边沿触发两种模式
select能并行支持I/O比较小,且无法修改
7KB
8KB
9KB
16KB
根据题意当拥塞窗口为16kb的时候发生了超时,那么接下来sshthresh也就是慢启动门限被设置为 16/2=8。cwud报文段被重置为1,那么超时之后的4个rtt会在第四个rtt的时候执行慢kaishi + 1 = 9

两者都属于自平衡二叉树
两者查找,插入,删除的时间复杂度相同
包含n个内部节点的红黑树的高度是O(log(n))
JDK的TreeMap是一个AVL的实现
1 好处 及 用途
红黑树 并不追求“完全平衡 ”——它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。
红黑树能够以 O(log2 n) 的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构 能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高。
当然,红黑树并不适应所有应用树的领域。如果数据基本上是静态的,那么让他们待在他们能够插入,并且不影响平衡的地方会具有更好的性能。如果数据完全是静态的,例如,做一个哈希表,性能可能会更好一些。
在实际的系统中,例如,需要使用动态规则的防火墙系统,使用红黑树而不是散列表被实践证明具有更好的伸缩性。
典型的用途是实现关联数组
2 AVL树是最先发明的自平衡二叉查 找树。在AVL树中任何节点的两个儿子子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis,他们在 1962 年的论文 "An algorithm for the organization of information" 中发表了它。
引入二叉树的目的是为了提高二叉树的搜索的效率,减少树的平均搜索长度.为此,就必须每向二叉树插入一个结点时调整树的结构,使得二叉树搜索保持平衡,从而可能降低树的高度,减少的平均树的搜索长度.
AVL树的定义:
一棵AVL树满足以下的条件:
1>它的左子树和右子树都是AVL树
2>左子树和右子树的高度差不能超过1
从条件1可能看出是个递归定义,如GNU一样.
性质:
1>一棵n个结点的AVL树的其高度保持在0(log2(n)),不会超过3/2log2(n+1)
2>一棵n个结点的AVL树的平均搜索长度保持在0(log2(n)).
3>一棵n个结点的AVL树删除一个结点做平衡化旋转所需要的时间为0(log2(n)).
从1这点来看 红黑树是牺牲了严格的高度平衡的优越条件 为 代价红黑树能够以O(log2 n)的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构 能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高.
霍夫曼树 必须是权值由小到大(由树叶到树根)!!!!
10S
20S
40S
100S
200S
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#include<stdint.h>#include<stdio.h>union X{ int32_t a; struct { int16_t b; int16_t c; };};int main(){ X x; x.a=0x20150810; printf("%x,%x\n",x.b,x.c); return 0;} |
2015,810 大端big-endian
50810,201
810,2015 小端little-endian
20150,810
TIME_WAIT
FIN_WAIT_1
SYNC_SENT
FIN_WAIT_2
、
、、毕竟开始建立连接也不能算是断开的啊!!!!!!!
1.自身对其(截止的长度是自身类型长度的整数倍)
2.整体对齐 (最长的类型 或者 parama pack指定的字节数)
原文:http://www.cnblogs.com/luntai/p/6411789.html