例子:
理论:
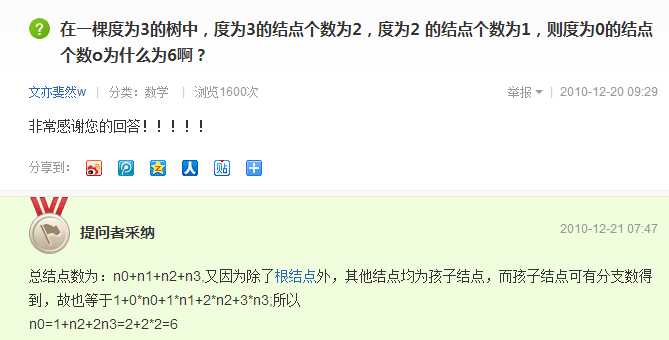
设叶结点数为n0,则树中结点数和总度数分别为
结点数=n0+n1+n2+...+nk
总度数=1×n1 + 2×n2 +...+ k×nk
根据树的性质结点数等于总度数加1,即
n0+n1+n2+...+nk = 1×n1 + 2×n2 +...+ k×nk + 1
得到叶结点数n0 = 1 + 1×n2 + 2×n3 +...+ (k-1)×nk
回楼主:n1+n2+...+nk不包括叶结点,叶结点的度为0
二叉树的度计算
有一个计算二叉树节点的公式,相信很多人都知道:
度为0的节点数为度为2的节点数加1,即n0=n2+1,知道这个公式,相关题目就可以轻松解决;
下面来讨论下如何得出这个公式的:
设:
k:总度数 k+1:总节点数 n0:度为0的节点 n1:度为1的节点 n2:度为二的节点
根据二叉树中度和节点的守衡原理,可列出以下一组方程:
k=n2*2+n1; k+1=n2+n1+n0;
将上面两式相减得到:n0=n2+1; 例【1】:已知767个节点的完全二叉树,求其叶子节点个数? 解析:
n0=n2+1; n=n0+n1+n2;
由上面,消掉n2得到:n=2n0+n1-1;
由于完全二叉树度为1的只有0个或1个两种情况,所以,将0或1带入上面公式,整理后得:
n0=(n+1)/2或者n0=n/2;
看看n是否能被2整除,能则用n0=n/2。否则用n0=(n+1)/2 既叶子节点为n0=(n+1)/2=384
例【2】:已知完全二叉树的结点有700个,求其叶子结点的个数? 解析:
完全二叉树,要求是除了最下面一层节点和部分倒数第二层节点外,所有节点均是满树。
因此我们可以得到以下满树的规律:
第一层:根节点 1个,即2^0个 第二层:两个,即:2^1个 第三层:4个,即:2^2个 ....
也就是说,n层满树的节点个数是: 2^0+2^1+2^2+...+2^(n-1)=2^n-1
所以:700个节点的完全二叉树最多10层 即第1-9层是满树,共有:511个节点
也就是说:第十层还有:700-511=189个节点,这些节点全叶子节点 于是完全二叉树,最后一层最多有一个节点不满, 所以第9层左边的95个节点是非叶子节点, 因此第九层有:256-95=161个有叶子节点 第十层有:189个叶子节点
因此共有:189+161=350个叶子节点
原文:http://www.cnblogs.com/wuyuankun/p/3750464.html