0-1背包问题描述
有一个窃贼在偷窃一家商店时发现有n件物品,第i件物品价值为vi元,重量为wi,假设vi和wi都为整数。他希望带走的东西越值钱越好,但他的背包中之多只能装下W磅的东西,W为一整数。他应该带走哪几样东西?
0-1背包问题中:每件物品或被带走,或被留下,(需要做出0-1选择)。小偷不能只带走某个物品的一部分或带走两次以上同一个物品。
部分背包问题:小偷可以只带走某个物品的一部分,不必做出0-1选择。
0-1背包问题解决方法
0-1背包问题是个典型具有公共子结构的问题,但是只能采用动态规划来解决,而不能采用贪心算法。因为在0-1背包问题中,在选择是否要把一个物品加到背包中,必须把该物品加进去的子问题的解与不取该物品的子问题的解进行比较。这种方式形成的问题导致了许多重叠子问题,满足动态规划的特征。动态规划解决0-1背包问题步骤如下:
0-1背包问题子结构:选择一个给定物品i,则需要比较选择i的形成的子问题的最优解与不选择i的子问题的最优解。分成两个子问题,进行选择比较,选择最优的。
0-1背包问题递归过程:设有n个物品,背包的重量为w,C[i][w]为最优解。即: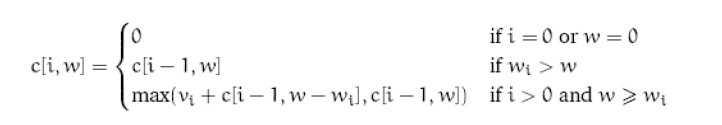
#include<iostream>
#include<algorithm>
#define MAX 1000
using namespace std;
int dp[MAX][MAX];
int record[MAX];
int W;
int KnapSack(int n,int w[],int v[])//物品个数n,物品的价值v[i],物品的重量w[i]
{
int i,j;
for(i=0;i<=n;i++)//初始化边界值
dp[i][0]=0;
for(j=0;j<=W;j++)
dp[0][j]=0;
for(i=1;i<=n;i++)
{
for(j=1;j<=W;j++)
{
if(j<w[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
}
}
//构造最优解
j=W;
for(i=n;i>0;i--)
{
if(dp[i][j]>dp[i-1][j])
{
record[i]=1;
j-=w[i];
}
else
record[i]=0;
}
return dp[n][W];
}
int main(int argc,char *argv[])
{
int n;
int i,j;
int v[MAX],w[MAX];
cout<<"Please input n= ";
cin>>n;
cout<<"Please input W= ";
cin>>W;
cout<<"Please input value: "<<endl;
for(i=1;i<=n;i++)
cin>>v[i];
cout<<"Please input weight: "<<endl;
for(j=1;j<=n;j++)
cin>>w[j];
cout<<"Max value is: "<<KnapSack(n,w,v)<<endl;
cout<<"Record: \n";
for(i=1;i<=n;i++)
cout<<" "<<record[i];
cout<<endl;
return 0;
}原文:http://blog.csdn.net/cstopcoder/article/details/26886991