一、思想
广度优先搜索(Breadth First Search),又称宽度优先搜索,简称广搜,BFS。是对图的一种遍历方式。
以这个无向带权图为例,结点上的数字为该结点的编号,边上的数字为该边的权值。
假如以结点1为源点,以结点7为目标结点,广度优先搜索扫描到结点的顺序应当是这样的。(如图,结点旁的红色数字表示搜到结点的顺序,对于由同一个结点引出的多个节点,按照字典序分别扫描。)
第一次,结点1。第二次,结点2。第三次,结点5。第四次,结点4。
第五次,结点6。第六次,结点7。第七次,结点3。
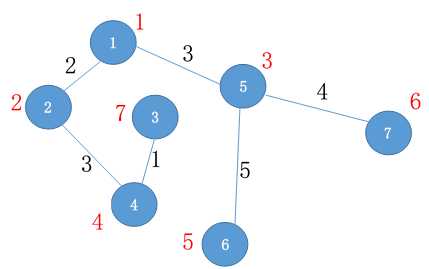
可以发现,它是从源点开始,对每一个与源点连通的点一一扫描,扫描完成后,对于扫描到的点,再按照每个点被扫描到的顺序,执行同样的操作。那么就有一个问题,对于扫描到的点,如何记录其被扫描到的顺序?答案是使用一种数据结构——队列。
把扫描到的结点按照扫描的顺序入队,一个结点引出的所有结点入队完成后,把该结点(即队头)出队,那么出队后的队头就是比它后一个进队(即后一个被扫描到)的结点。
若共有n个结点,用a[i][j]表示图中结点i到结点j的权值(假设没有负权和为0的权),若结点i到结点j无边,那么令a[i][j]=0,用Q来表示该队列,h表示队头所表示的结点,pop表示队头出队,push(i)表示结点i进队,empty表示该队列是否为空,为空则返回0。那么从源点s到终点e,广度优先搜索的伪代码可以写成:
BFS1
Q.push(s);
while not Q.empty
for j = 1 to n do
if not a[i][j] = 0
Q.push(j);
Q.pop;
这段代码会把整个图搜索一遍,但是我们要求搜索到终点,在实际的应用中,往往是要输出方案或者能否搜索到终点,所以这段代码是有问题的。
因此,我们在搜索到每个结点(在代码中即该结点入队)时,要判断该结点是否为目标结点,而为了达到这个目的,只要修改一下push就可以了
下面给出在结点入队时判断是否为目标结点的代码(搜到目标结点后输出’T’并结束程序):
push1(i)
if i = e
print(“T”);
while not Q.empty
Q.pop;
else
push(i);
相应地,原来的代码中push(i);的部分也要改为push1(i);
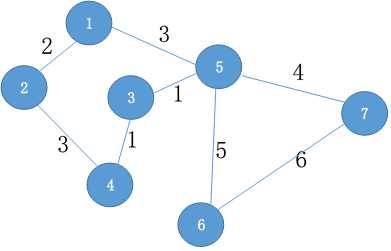
对于与上面的图相类似的无环图,这样的方法可以适用,但是如果在上图的3,5结点间加一条边(如图),6,7结点间加一条边,那么这幅图成为有环的图。
用同样的方法,我们来模拟一下。
首先结点1进队,队列:1
然后结点2,5进队,1出队,队列:2 5
然后结点4进队,2出队,队列:5 4
然后结点1,3,6,7进队,5出队,队列:4 1 3 6 7(结点1又进队了?)
然后结点2,3进队,4出队,队列:1 3 6 7 2 3(结点2,3又进队了?队里有两个3?)
……
不难发现,按照同样的方法,对于有环的图来说,有环上的结点会重复进队,假如用一个数组来储存队列的话,相对于无环图,将会增加很大的空间开销。
所以,要防止结点重复进队,但是怎样防止呢?很明显,所有的结点可以分为两类:进过队的(注意:是进过,不是在队内,因为有结点出队)和没进过队的,那么使用布尔数组b来储存结点是否进过队,假如结点i进过队,就令b[i]=true,那么b[i]要全部初始化为false。
下面给出防止结点重复进队的代码和函数push3:
BFS1
b[1..n]=false;
Q.push(s);
while not Q.empty
for j = 1 to n do
if not a[Q.h][j] = 0
Q.push2(j);
Q.pop;
push2(i)
if b[i]=true
return;
b[i]=true;
if i = e
print(“T”);
while not Q.empty
Q.pop;
else
push(i);
二、例题
题目描述
考虑将如此安排在一个 3 * 3 行列中的九个时钟:
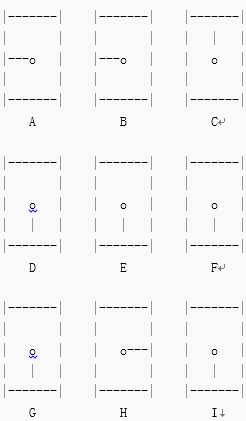
目标要找一个最小的移动顺序将所有的指针指向12点。下面原表格列出了9种不同的旋转指针的方法,每一种方法都叫一次移动。选择1到9号移动方法,将会使在表格中对应的时钟的指针顺时针旋转90度。
移动方法 受影响的时钟
1 ABDE
2 ABC
3 BCEF
4 ADG
5 BDEFH
6 CFI
7 DEGH
8 GHI
9 EFHI
输入
9个数字,代表各个钟的初始状态
输出
把所有的钟指向12点的最短移动方案
输入样例
9 9 12
6 6 6
6 3 6
输入样例
4 5 8 9
对于这样一道题目,首先分析是否可以用广搜,广搜是一种图的遍历方式,那么就要知道图是怎么样的,源点是什么,以及目标结点是什么。显而易见地,源点应该是各个钟的最初状态,可以使用一个数组来储存。既然源点是一个状态,那么每个结点也是一个状态,即所有钟的指针指向。目标结点就是所有钟都指向12点的状态。
从任意一个结点出发,引出的结点(也就是经过1次移动后变成的状态)个数明显与移动方法的种数相同,即9种。
使用常数数组a[9][9]来储存移动的方法,a[i][j]表示第i种方法对第j个钟是否有影响。
那么根据题意,a可以初始化为{{1, 1, 0, 1, 1, 0, 0, 0, 0}, {1, 1, 1, 0, 0, 0, 0, 0, 0}, {0, 1, 1, 0, 1, 1, 0, 0, 0}, {1, 0, 0, 1, 0, 0, 1, 0, 0}, {0, 1, 0, 1, 1, 1, 0, 1, 0}, {0, 0, 1, 0, 0, 1, 0, 0, 1}, {0, 0, 0, 1, 1, 0, 1, 1, 0}, {0, 0, 0, 0, 0, 0, 1, 1, 1}, {0, 0, 0, 0, 1, 1, 0, 1, 1}}
使用b[4][4][4][4][4][4][4][4][4]来储存结点是否进过队,
b[i1][i2][i3][i4][i5][i6][i7][i8][i9]表示9个钟状态为i1,i2,i3,i4,i5,i6,i7,i8,i9的结点是否进过队。用结构体point来储存结点,每个结点包括以下几个信息:
f表示它的父结点,即它由哪个结点扩展而来。
x表示该结点的钟的状态。
c表示扩展至该结点的移动方法。
为什么要有f呢?在输出方案的时候需要从目标结点往回找,所以需要父结点。
为什么要有x呢?在扩展到这个结点的子节点时需要这个结点的状态。
为什么要有c呢?这还用问。。。要求输出的就是移动方法。
用结构体数组q来表示队列,h是队头指针,t是队尾指针,那么出队就是h++,入队就是t++并把入队结点的信息存在q[t]里面。
这个q数组要开多大呢?这取决于结点有几个,即状态有几种,9个钟每个有4个状态,那么就有4^9=262144种。所以q数组只要开得比这个大就可以了,比如300000。
在读入初始状态信息时,先把它入队,然后按照广搜的方法一一做。
在入队的push过程中,如果已经入过队,那么就直接跳出,如果没有,就把它入队,在判断一下该结点是否为目标结点,如果是,就从该结点开始,找到父结点,再找父结点的父结点,一直找到源点,每到一个点,就把它的移动方法(c)储存下来,结束后再倒序输出。
原文:http://www.cnblogs.com/zkx06111/p/3536830.html