Linear Regression（一）——

定义

回归的定义

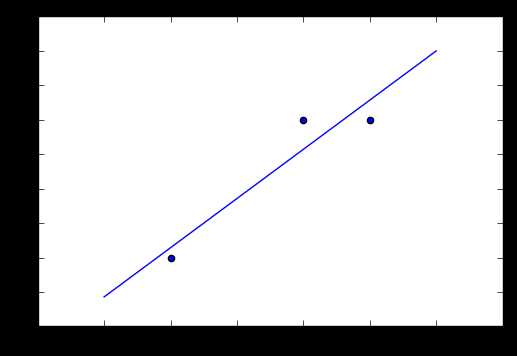
在平面上存在这些点我希望能用一条直线尽可能经过它们。

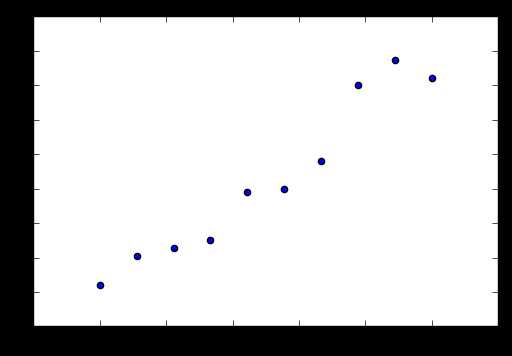
于是我们画了下面的一条直线

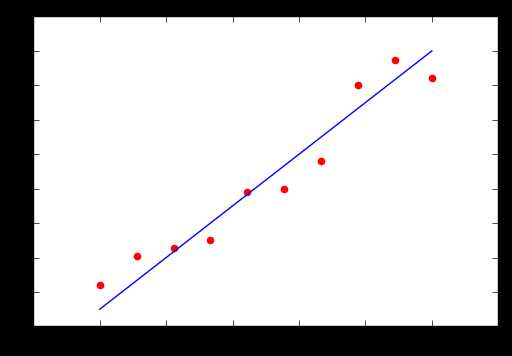
这样的过程就叫做回归。

这个过程中我们的目的其实就是寻找输入变量（自变量）和输出变量的关系（因变量）

线性回归的定义

线性回归：上图中我们进行的回归就是线性回归
线性回归实际上是假设输入变量x和输出变量y存在着这样的关系
在刚刚的情况下，横坐标为,那么公式上图可以表示为,w实际上是这样的一个矩阵,而x实际上是的这样一个矩阵,二者相乘即

线性回归模型

损失函数

我们已经知道了线性回归的定义，那么如何寻找这样的一条直线呢？什么样的直线是最好的？

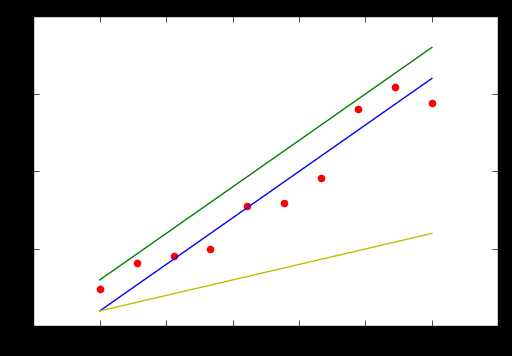
这张图我们可以明显的看出蓝色的直线是最优的，我们判断的依据是什么？就是直线到各个点的距离
因此我们引出了损失函数
损失函数：
各样本的输出，各变量权重，输入变量

我们的目的即最小化损失函数，使得到的直线到各点的距离最小

损失函数最小化

最简便求得损失函数最小值的方法当然是求导，因此我们以一元线性模型进行说明
存在如下样本训练集T={(3,3),(4,3),(1,1)}，求出它的回归直线
我们可以得到以下公式

我们的目标是的最小化
对分别求a,b的偏导得


另两个偏导等于0可以求得a,b
*a=0.71428571,b=0.42857143
使用matplotlib画出图像

使用最小二乘法求得最优解

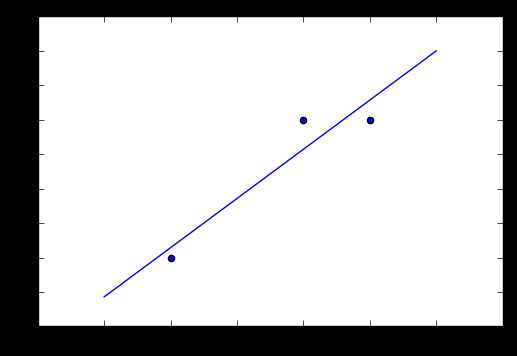
上文对于一元线性回归方程使用基础的数学方法可得出结果，当求解多元线性回归方程，为了计算的简便，我们通常会将数据转化为矩阵，通过最小二乘法求出数据的结果。
我们已经知道损失函数的矩阵形式表示为

那么我们使用矩阵的求导方法即可得出最优的W
Wiki已经给出了推导，对于没有梯子的可以参照该博文最小二乘法的矩阵形式推导

通过最小二乘法我们得出最优的w为

# X,Y以上文举例分别为[3,2],[3,1]的矩阵
import numpy as np
X = [[3,1],[4,1],[1,1]]
Y= [[3],[3],[1]
X = np.mat(X)
Y = np.mat(Y)
w = (X.T*X).I*X.T*Y

下载.png