Bellman-Ford算法在每实施依次松弛后,就会有一些顶点已经求得最短路,此后这些顶点的最短路的估计值就会一直不变,不再收后续松弛操作的影响,但是每次还要判断是否需要松弛,这就浪费时间了。
从上面可以得到启发:每次仅对最短路估计值发生变化了的顶点的所有出边执行松弛操作。
but,如何知道当前哪些点的最短路程发生了变化呢?
这里可以用一个队列来维护这些点,算法大致如下:
每次选取队首顶点u,对顶点u的所有出边进行松弛操作。例如有一条u->v的边,如果通过u->v这条边使得源点到顶点v的最短路程变短
(dis[u]+e[u][v]<dis[v]),且顶点v不在当前的队列中,就将顶点v放入队尾。
需要注意的是,同一个顶点同时在队列中出现多次是没有意义的,所以需要一个数组来判重(判断哪些点已经在队列中)。
在对顶点u的所有出边松弛完毕后,就将顶点u出队。
接下来不断从队列中取出新的队首顶点再进行如上操作,直到队列空为止。
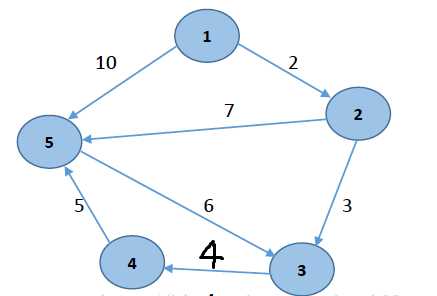
对于上图,采用队列优化的方法求得最短路径。
下面是代码实现,用邻接矩阵来存储这个图,具体如下:
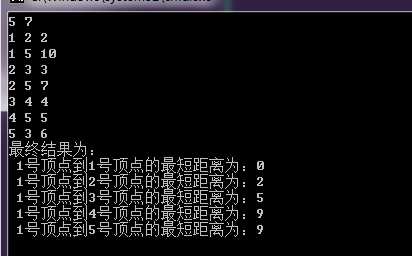
#include <stdio.h> #define INF 999999 int book[10]; //初始化为顶点都不在队列 int que[100]; // 松弛成功并且顶点不在队列则并入队列 int main(int argc, char const *argv[]) { int i, j, n, m; int q1, q2, q3; int dis[10], e[10][10]; int head, tail; //读入n和m,n表示顶点个数,m表示边的个数 scanf_s("%d %d", &n, &m); //初始化邻接矩阵 for (i = 1; i <= n; ++i) { for (j = 1; j <= n; ++j) { if (i == j) { e[i][j] = 0; } else { e[i][j] = INF; } } } //输入边 for (i = 1; i <= m; ++i) { scanf_s("%d %d %d", &q1, &q2, &q3); e[q1][q2] = q3; } //初始化dis数组 for (i = 1; i <= n; ++i) { dis[i] = INF; } dis[1] = 0; //初始化dis[1]为0,其他为∞ head = tail = 1; que[tail] = 1; //1号顶点入队 tail++; book[1] = 1; //标记1号顶点已经入队 while (head < tail) //队列不为空的时候循环 { for (i = 1; i <= n; ++i) { if (e[que[head]][i] != INF && dis[i] > dis[que[head]] + e[que[head]][i]) { dis[i] = dis[que[head]] + e[que[head]][i]; if (!book[i]) //顶点不在队列,加入队列 { book[i] = 1; que[tail++] = i; } } } //出队 book[que[head]] = 0; //重新标记不在队列 head++; //相当于出队 } printf("最终结果为:\n"); for (i = 1; i <= n; ++i) { printf(" 1号顶点到%d号顶点的最短距离为:%d\n", i, dis[i]); } printf("\n"); getchar(); getchar(); return 0; }
原文:http://www.cnblogs.com/lxt1105/p/6478108.html