最大连续和问题

　　最大字段和问题虽然简单，但蕴含了很多算法的思想，包括动态规划和分治法。

问题描述

最大连续和问题  给出一个长度为n的序列A₀,A₁,...,A_n-1，求最大连续和。也就是，要求找到一组(i,j)满足0≤i≤j≤n-1，使得A_i+A_i+1+...+A_j尽量大。

解法1 暴力枚举

　　我们可以枚举出所有的连续和，记B(i,j)=A_i+A_i+1+...+A_j，也就是 i 从0取到n-1，j 从 i 取到n-1。因此，我们要做的分为两部分，第一部分是枚举出所有的B(i,j)，第二部分是对于具体的B(i,j)计算它的值，那么时间复杂度\(T(n)=\sum_{i=0}^{n-1}\sum_{j=i}^{n-1}(j-i+1)=\frac{n(n+1)(n+2)}{6}=\Theta(n^3)\)。

　　具体实现如下（python代码）

def get_max_continue_sum(A):
    n=len(A)
    best=A[0]
    for i in xrange(n):
        for j in xrange(i,n):
            B_ij=sum(A[i:j])
            if best<B_ij:
                best=B_ij
    return best

一点改进方法

　　这里包含一点动态规划的思想。

　　计算连续和的时候，我们使用公式B(i,j)=A_i+A_i+1+...+A_j。也就是说，我们需要j-i+1步才能计算出B(i,j)，但是这是没有必要的。

　　设前缀和S(i)=A₀+A₁+...+A_i，那么有B(i,j)=S(j)-S(i-1)。有了这个式子，我们就可以通过前缀和计算连续和。改进后的算法的时间复杂度\(T(n)=\Theta\)

　　具体代码如下

def get_max_continue_sum(A):
    n=len(A)
    S=[A[0]]
    for i in xrange(1,n):
        Si=S[i-1]+A[i]
        S.append(Si)

    best=A[0]
    for i in xrange(n):
        for j in xrange(i,n):
            B_ij=S[j]-S[i-1]
            if best<B_ij:
                best=B_ij
    return best

解法2 分治法

　　分治的英文是Divide and Conquer，也就是将问题划分为多个子问题，然后分别解决。

思路  对于一个序列{A₀,A₁,...,A_n-1}中的一个元素A_k，假设最大字段和为B(i,j)，那么存在两种情况，A[i:j]要么包括A_k，要么不包括A_k。如果A[i:j]要么包括A_k，那我们怎么求B(i,j)呢？B(i,j)=B(i,k-1)+A_k+B(k+1,j)，这也就是说，通过一遍扫描，就求出包含元素k的最大字段和，时间花费为\(O(n)\)（原本会花费\(O(n^2)\)的时间，想一想为什么）。　　

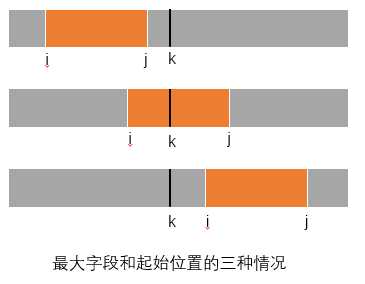
　　于是，我们将一个序列划分为左半和右半两部分，分别求出相应的最大字段和B₁和B₂，同时求出起点位于左半、终点位于右半的最大连续和B3，那么该序列的最大字段和B=max(B₁,B₂,B₃)。

　　比如序列{-2,4,5,-1,-6,9,-1,3}，我们将它划分为两部分{-2,4,5,-1}和{-6,9,-1,3}，那么B₁=4+5=9,B₂=9,B₃=(4+5-1)+(-6+9)=11，因此B=max(9,9,11)=11。

　　要说明的是，在求B₁和B₂时，我们使用的方法是调用函数本身。因此，此方法的时间复杂度\(T(n)\)满足\(T(n)=T(n/2)+O(n)\)，解得\(T(n)=nlog(n)\)。

　　具体实现如下

#python 2.7
def get_max_continue_sum(A):
    n=len(A)
    k=n/2
    B1=get_max_continue_sum(A[:k])
    B2=get_max_continue_sum(A[k:])
    
    L_best=_get_best_of_left(A[:k])
    R_best=_get_best_of_right(A[k:])
    B3=L_best+R_best
    
    return max(B1,B2,B3)
    
def _get_best_of_left(A):
    n=len(A)
    v=A[-1]
    best=v
    for i in xrange(n-2, 0 ,-1):
        v+=A[i]
        best=max(best,v)
    return best

def _get_best_of_right(A):
    n=len(A)
    v=A[0]
    best=v
    for i in xrange(1, n):
        v+=A[i]
        best=max(best,v)
    return best

解法3  动态规划法

最大连续和问题

原文：http://www.cnblogs.com/super-zhang-828/p/6437749.html