0-1背包问题:
有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
这个问题用穷举法当然可以做,但是用动态规划所用的时间花销更少,但是要用一个二维数组存储局部最优值,最后达到总的最优值,可以说是用空间换时间,非常的经典!
直接贴c++代码:
//动态规划 本程序是自底向上自左向右更新最优值 #include<iostream> using namespace std; int main() { int c=10; //总的承重量,好像没有用到,因为j也可以表示 int m[6][11]={0}; // 第一行与第一列不用,方便编程,表示需要更新的二维数组 int w[6]={0,2,2,6,5,4}; //多写个0方便编程,物品的重量 int v[6]={0,6,3,5,4,6}; //同上,物品的价值 for(int i=5;i>=1;i--) //循环五次,动态尝试放入五个物品 for(int j=1;j<=10;j++) { if(i==5) //最后一行不依赖其它行更新最优值,因为表示的是第一个放入背包的物品 { if(w[5]<=j) {m[i][j]=v[5];} } else{ if(w[i]>j) //动态规划核心,此式子选择动态更新局部最优值 { m[i][j]=m[i+1][j]; //动态规划核心,此式子选择动态更新局部最优值 } else { m[i][j] =m[i+1][j]>m[i+1][j-w[i]]+v[i]?m[i+1][j]:m[i+1][j-w[i]]+v[i]; //动态规划核心,此式子选择动态更新局部最优值,
//等价于m[i][j]=max{m[i+1][j],m[i+1][j-w[i]]+v[i]} } } } cout<<m[1][10]<<endl;//输出最大价值总和,因为本程序是自底向上自左向右更新最优值,所以最大价值总和在第一行第十列(右上角)。 for(int i=1;i<=5;i++) //循环输出更新后的二维数组 for(int j=1;j<=10;j++){ cout<<m[i][j]; cout<<" "; if(j==10) cout<<endl; } return 0; }
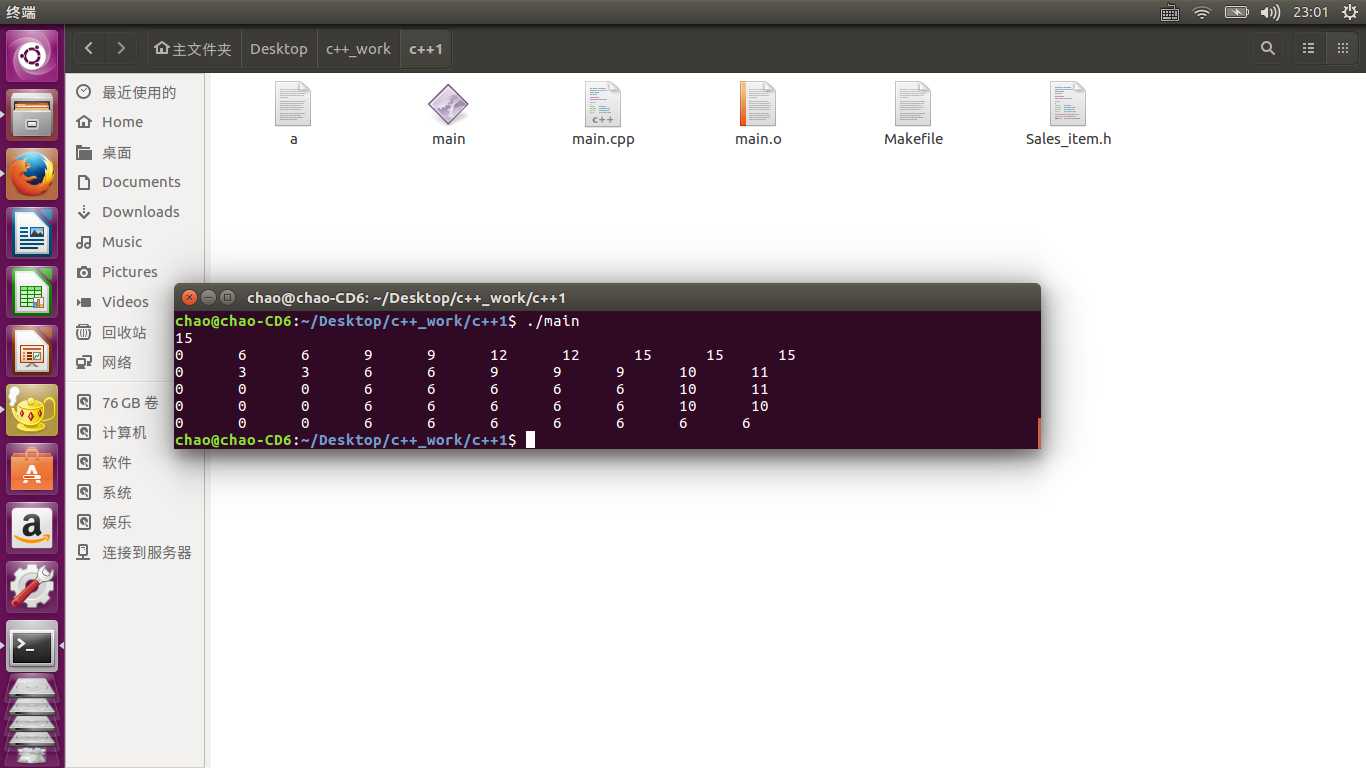
运行效果图以及自底向上自左向右更新后的二维数组如下:
原文:http://www.cnblogs.com/lcbg/p/6481559.html