


3
2 2 1


由于是带标号的无根树的计数,于是我们运用prufer编码的性质来解题。
prufer编码的几个性质:
1.对于大小为s的树,prufer编码是一个长度为 s-2 的序列;
2.i在序列中出现的次数<deg[i];
3.一个prufer编码表示一棵树。
所以这题可以转化为求prufer编码的计数。
我们令f[i][j][k]表示前i个点,选择了j个,prufer编码长度为k的方案数。那么显然有
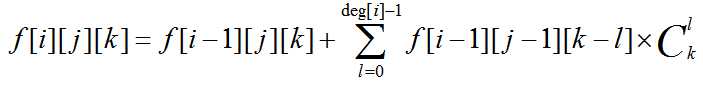
其中 f[i-1][j][k] 表示不选择该点的方案数,后面的式子表示选择了该点的方案数,选择该点可以在编码中出现0-deg[i]-1次,然后在编码中的出现顺序可以任意所以要乘上C。
最后如果i=1显然输出n,否则由于prufer编码是长度i-2的序列,所以输出f[n][i][i-2]。

1 #include<iostream>
2 #include<string>
3 #include<algorithm>
4 #include<cstdio>
5 #include<cstring>
6 #include<cstdlib>
7 #include<vector>
8 #include<cmath>
9 using namespace std;
10 typedef long long s64;
11 const int ONE=105;
12 const int MOD=1004535809;
13
14 int n;
15 int deg[ONE];
16 int C[ONE][ONE];
17 int f[ONE][ONE][ONE];
18
19 int get()
20 {
21 int res=1,Q=1;char c;
22 while( (c=getchar())<48 || c>57 )
23 if(c==‘-‘)Q=-1;
24 res=c-48;
25 while( (c=getchar())>=48 && c<=57 )
26 res=res*10+c-48;
27 return res*Q;
28 }
29
30 void Mod(int &a)
31 {
32 if(a>MOD) a-=MOD;
33 }
34
35 int main()
36 {
37 n=get();
38 for(int i=1;i<=n;i++) deg[i]=get();
39
40 C[0][0]=1;
41 for(int i=1;i<=n;i++)
42 {
43 C[i][0]=1;
44 for(int j=1;j<=n;j++)
45 C[i][j] = (C[i-1][j] + C[i-1][j-1]) % MOD;
46 }
47
48 f[0][0][0]=1;
49 for(int i=1;i<=n;i++)
50 for(int j=0;j<=i;j++)
51 for(int k=0;k<=n;k++)
52 {
53 f[i][j][k] += f[i-1][j][k]; Mod(f[i][j][k]);
54 if(!j) continue;
55 for(int l=0; l < deg[i] && l <= k ;l++)
56 {
57 f[i][j][k] += (s64)f[i-1][j-1][k-l] * C[k][l] % MOD;
58 Mod(f[i][j][k]);
59 }
60 }
61
62 for(int i=1;i<=n;i++)
63 {
64 if(i==1) printf("%d ",n);
65 else printf("%d ",f[n][i][i-2]);
66 }
67 }
原文:http://www.cnblogs.com/BearChild/p/6486405.html