作者:桂。
时间:2017-03-09 21:15:34
链接:http://www.cnblogs.com/xingshansi/p/6527961.html
声明:欢迎转载,不过记得注明出处哦~

未完待续...
【读书笔记01】
前言
|
这几天打算学一学滤波器的相关原理,看的书籍是西蒙.赫金的《自适应滤波器原理》第四版,记录的内容为自己的学习总结,本文主要分为以下四部分: 1)随机过程、确定过程 2)均值、方差、分布函数与概率密度 3)不相关与独立性 4)平稳性与遍历性 内容中不当的地方,还麻烦各位给以指正,内容多有参考他人,对应的链接在文章最后一并给出。 |
一、随机过程与确定过程
对于一个火车,下一时刻的轨迹已经由铁轨确定了;而对于一个行人,下一刻的落脚点却有各种可能。
简单来说,下一时刻确定的,是确定过程;不确定的,是随机过程。
给一张示意图:
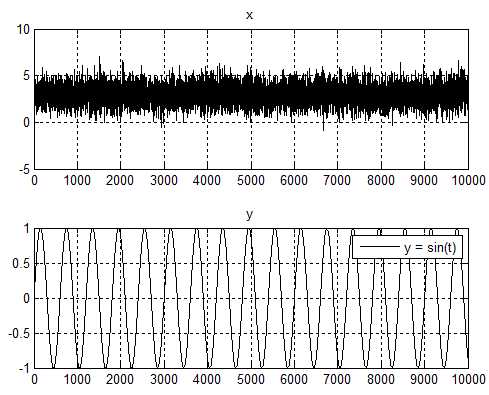
信号x是一个随机分布,下一刻的值有各种可能;而信号y是一个确定过程,下一刻的值由$y = sin(t)$唯一确定。
既然有各种可能,为什么还要研究随机过程呢?再来一个示意图:
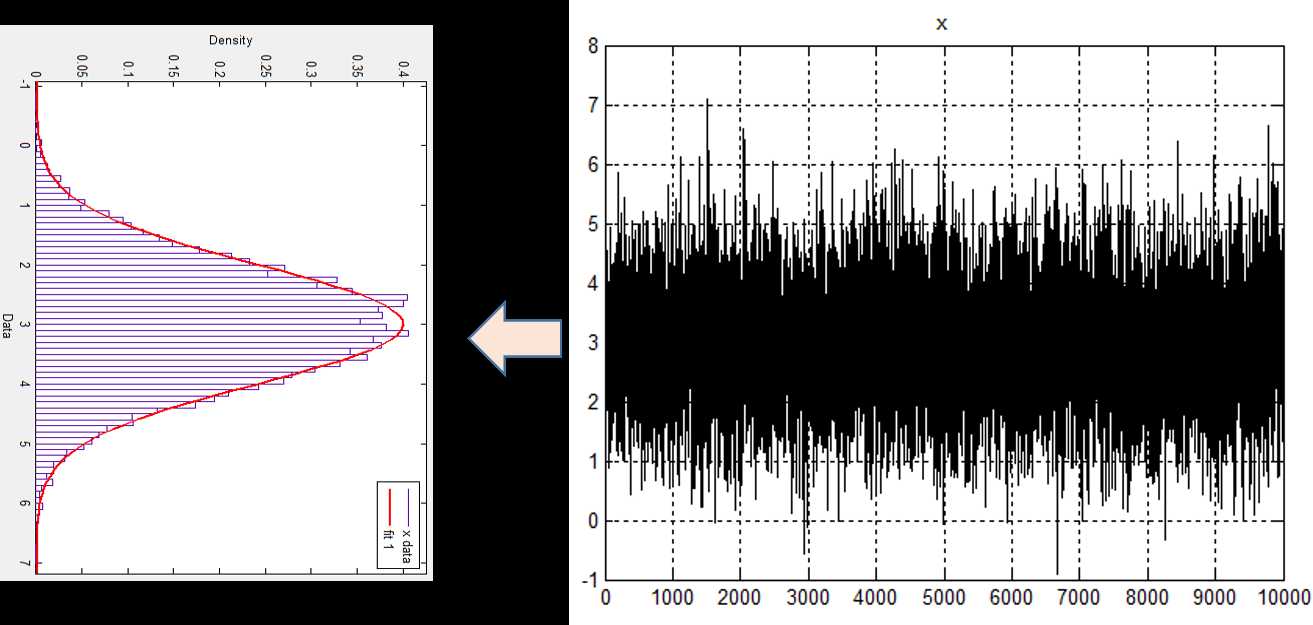
将随机信号x进行直方图统计,通过曲线拟合可以看到:x对应的每一时刻的值都服从正态分布,我们或许可以说:下一时刻,信号x取3的概率大于x取9的概率。由此我们可以相信:对于随机的数据,直方图统计也会包含有价值的信息,so~继续研究它。
二、常用基本概念
A-均值
给出均值的定义式:
$E[x(t)] = \int_{\; - \infty }^{\; + \infty } {x{f_X}(x\;;t)} dx$
即对于给定时刻t,假设所有的可能都给定了,我们不需要像上一张图那样,需要对不同时刻t进行统计,而是直接对t时刻所有可能值统计,得到分布直方图。利用分布的密度函数,从而实现均值的估计。
现实情况是:我们无法得到同一时刻的所有可能,怎么解决这个尴尬?接着往下看。
B-方差
假设$\mu (t)$是t时刻的均值,则对应的方差定义为:
$D[x(t)] = \int_{\; - \infty }^{\; + \infty } {{{(x - \mu (t))}^2}{f_X}(x\;;t)} dx$
求解同均值类似,尴尬也是。
C-分布函数与概率密度
直接对t时刻所有可能值统计,得到分布直方图,直方图面积归一化,对应的曲线就是概率密度$f(x;t)$,$f(x;t)$关于x的积分就是分布函数$F(x;t)$。
三、不相关与独立性
给一个示意图:
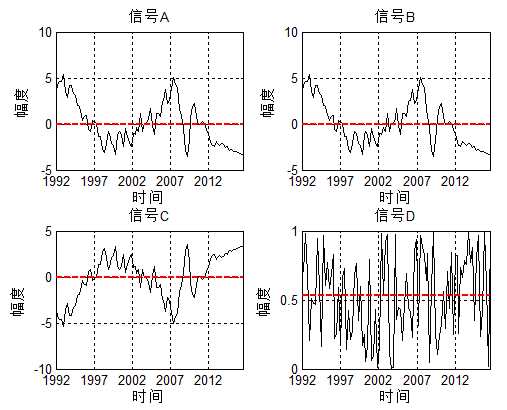
信号A、B、C、D是四个不同的随机信号:
给出定义式:
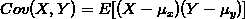
关于相关的细节讨论,可以参考知乎的答案。
从定义式也可以观察:此处的相关是线性相关,而不是统计相关。因此即使不相关,也不过是线性不相关罢了,说的简单点:A、B两信号不相关,则A的取值变化,不对B的取值产生影响。
给一个示意图:
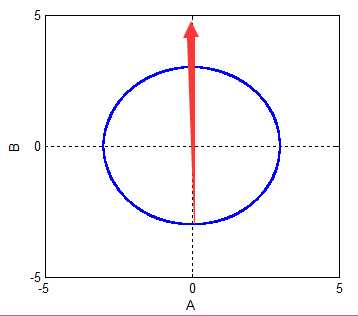
可见A取值的增加/减小,与B的增加/减小,无关。即:A、B的线性变化趋势无关;但A的取值对B的取值分布,存在影响。独立则一定线性不相关,线性不相关,不一定独立。
四、平稳性与遍历性
参考:
原文:http://www.cnblogs.com/xingshansi/p/6527961.html