目录
何为BellmanFord算法?
Floyd算法功能:给定一个加权连通图,选取一个顶点,称为起点,求取起点到其它所有顶点之间的最短距离,其显著特点是可以求取含负权图的单源最短路径。
Floyd算法思想:
Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E)。(V为给定图的顶点集合,E为给定图的边集合)
本文编码思想主要参考自文末参考资料1中博客,想要进一步了解,可以参考文末参考资料。
首先看下代码中所使用的连通图(PS:改图为无向连通图,所以每两个顶点之间均有两条边):
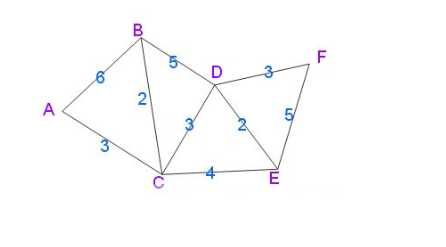
现在求取顶点A到其它所有顶点之间的最短距离
具体代码如下:
package com.liuzhen.chapter9; import java.util.Scanner; public class BellmanFord { public long[] result; //用于存放第0个顶点到其它顶点之间的最短距离 //内部类,表示图的一条加权边 class edge { public int a; //边的起点 public int b; //边的终点 public int value; //边的权值 edge(int a, int b, int value) { this.a = a; this.b = b; this.value = value; } } //返回第0个顶点到其它所有顶点之间的最短距离 public boolean getShortestPaths(int n, edge[] A) { result = new long[n]; for(int i = 1;i < n;i++) result[i] = Integer.MAX_VALUE; //初始化第0个顶点到其它顶点之间的距离为无穷大,此处用Integer型最大值表示 for(int i = 1;i < n;i++) { for(int j = 0;j < A.length;j++) { if(result[A[j].b] > result[A[j].a] + A[j].value) result[A[j].b] = result[A[j].a] + A[j].value; } } boolean judge = true; for(int i = 1;i < n;i++) { //判断给定图中是否存在负环 if(result[A[i].b] > result[A[i].a] + A[i].value) { judge = false; break; } } return judge; } public static void main(String[] args) { BellmanFord test = new BellmanFord(); Scanner in = new Scanner(System.in); System.out.println("请输入一个图的顶点总数n和边总数p:"); int n = in.nextInt(); int p = in.nextInt(); edge[] A = new edge[p]; System.out.println("请输入具体边的数据:"); for(int i = 0;i < p;i++) { int a = in.nextInt(); int b = in.nextInt(); int value = in.nextInt(); A[i] = test.new edge(a, b, value); } if(test.getShortestPaths(n, A)) { for(int i = 0;i < test.result.length;i++) System.out.print(test.result[i]+" "); } else System.out.println("给定图存在负环,没有最短距离"); } }
运行结果:
请输入一个图的顶点总数n和边总数p: 6 18 请输入具体边的数据: 0 1 6 0 2 3 1 2 2 1 3 5 2 3 3 2 4 4 3 4 2 3 5 3 4 5 5 1 0 6 2 0 3 2 1 2 3 1 5 3 2 3 4 2 4 4 3 2 5 3 3 5 4 5 0 5 3 6 7 9
参考资料:
算法笔记_070:BellmanFord算法简单介绍(Java)
原文:http://www.cnblogs.com/liuzhen1995/p/6533431.html