树(Tree)是n(n>=0)个结点的有限集。 n = 0 时成为空树。在任意一颗非空树中:
(1). 有且仅有一个特定的成为根(root)的节点。
(2). 当 n > 1 时,其余结点可以分为m个互不相交的有限集 T1、 T2、 T3 .....Tm,其中每一个集本身又是一棵树,并且称为根的子树。
在一棵树中,结点分为 根结点、内部结点和叶结点(又称终端结点)。
结点拥有的子树的数目称为结点的度(Degree)。 B的度为1, D的度为3
在一棵树中, 最大的结点的度为树的度。 由于D的度最多,所以树的度就是3.
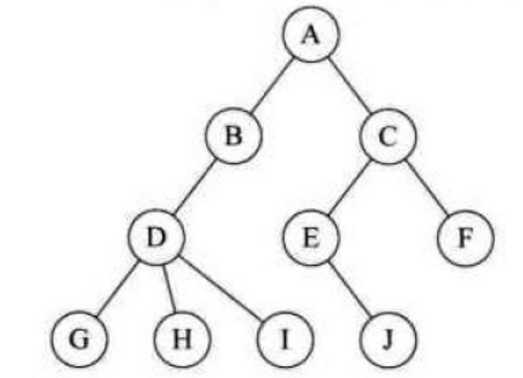
其中B是A的孩子, A是B的双亲, C是B的兄弟。 之所以称之为双亲是因为对于结点来说父母同体,只有这么称呼是比较合适的了。
3. 其他相关概念
结点的层次: 从根开始算起, 根为第一层,然后第二层,第三层....
树的深度或高度: 结点的最大层次就是树的深度或高度。
有序树:如果将树中结点的各子树看成是从左到右有次序的,不能互换的,那么该树就是有序树,否则就是无序树。
原文:http://www.cnblogs.com/zhuzhenwei918/p/6533381.html