1、三路快速排序算法的基本思想
之前的快速排序算法都是将序列分成<=v和>v或者是<v和>=v的两个部分,而三路快速排序是将序列分成三个部分:
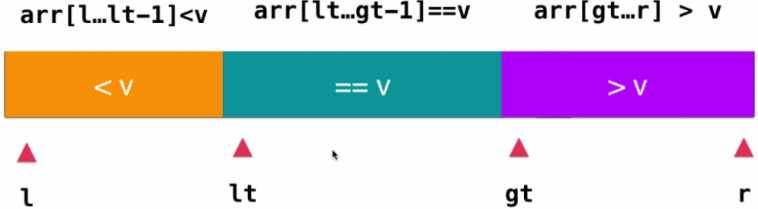
<v、=v、>v,如下图所示:

首先v元素还是作为"基准"元素,e表示当前遍历索引值指向的元素,也就是待考虑的元素,从图中可以看出来,整个序列被分成
3个部分,也就是说当我们遍历完成之后整个序列就已经被分成了<v、=v、>v三个部分了,而我们只需要对<v和>v的两个部分
再次递归调用三路排序函数进行排序即可,来看看具体的过程:
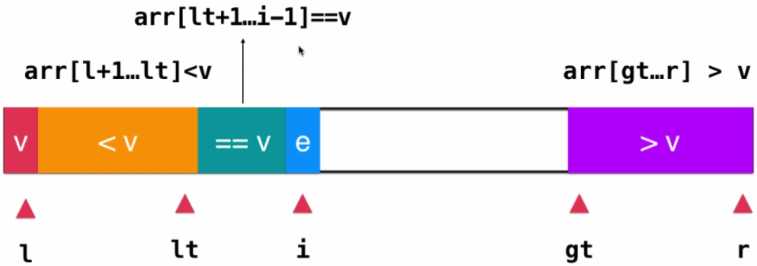
首先来看看整个序列的布局,这里我们使用了3个索引值来表示3个不同的位置,使用lt索引来表示<v部分和=v部分的分界处(这里
选的是<v部分的最后一个元素),使用i索引表示遍历的位置,使用gt索引来表示=v部分和>v部分的分界处(这里选的是>v部分的
第一个元素)。
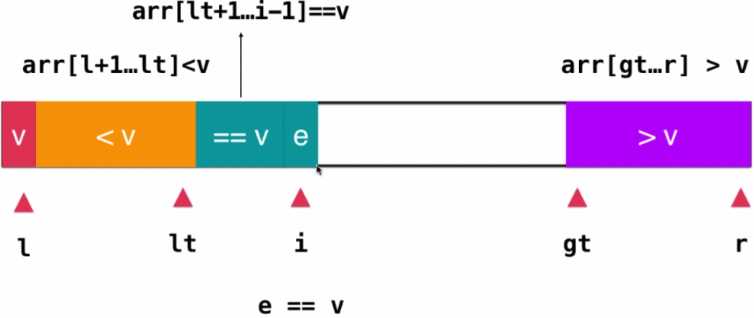 如果当前i指向的元素=v,那直接就将此元素归为=v部分,i++即可
如果当前i指向的元素=v,那直接就将此元素归为=v部分,i++即可
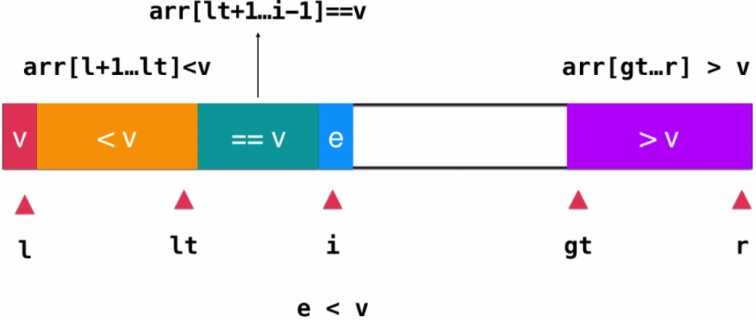 如果当前i指向的元素<v,将此元素与=v部分的第一个元素交换位置,
如果当前i指向的元素<v,将此元素与=v部分的第一个元素交换位置,
也就是swap(arr[i], arr[lt+1]),之后将lt++, i++即可,此时<v部分就
多了一个元素
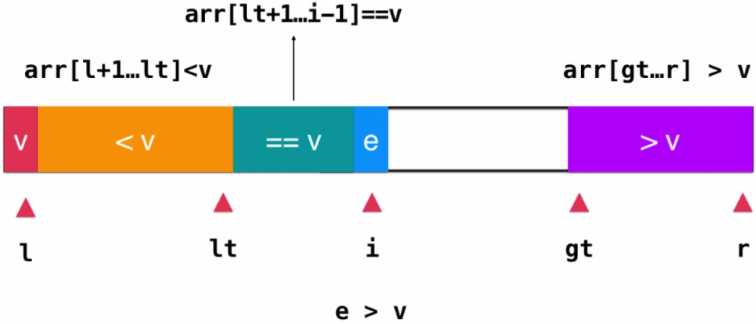 如果当前i指向的元素>v,则将此元素与>v部分的第一个元素的前一个元素交换
如果当前i指向的元素>v,则将此元素与>v部分的第一个元素的前一个元素交换
位置,也就是swap(arr[i], arr[gt-1]),然后gt--,表示>v部分多了一个元素
此时i不用动,因为他指向的元素是交换过来的,这个元素还没有遍历到。
 当gt与i重合的时候就表示便利完毕了,那么此时我们只需要将l指向的元素v与lt交换
当gt与i重合的时候就表示便利完毕了,那么此时我们只需要将l指向的元素v与lt交换
位置即可,之后就如下所示了
之后我们只需要对<v和>v这两部分再次递归进行三路排序,而对于=v的部分就不用在考虑了,因为他们已经放在了合适的位置了,所以从这
里可以看出来如果=v部分元素非常多,那么我们的三路快速排序算法效果就会越明显,这也正是他的优点所在。
2、三路快速排序算法的实现(基于C++)
首先说明,代码中使用到的索引值变量都是取之于上面的图示中,这样便于描述问题
1 /**************************************三路快速排序算法实现***********************************/ 2 template<typename T> 3 void __quickSort3Ways (T arr[], int left, int right) 4 { 5 if (right - left <= 40) { /* 对递归到数据量较小时使用插入排序 */ 6 __insertSortMG<T>(arr, left, right); 7 return; 8 } 9 10 std::swap(arr[left], arr[std::rand() % (right - left + 1) + left]); // 随机化找到一个元素作为"基准"元素 11 T v = arr[left]; 12 13 int lt = left; // 将<v的分界线的索引值lt初始化为第一个元素的位置(也就是<v部分的最后一个元素所在位置) 14 int gt = right + 1; // 将>v的分界线的索引值gt初始化为最后一个元素right的后一个元素所在位置(也就是>v部分的第一个元素所在位置) 15 int i = left + 1; // 将遍历序列的索引值i初始化为 left+1 16 17 while (i < gt) { // 循环继续的条件 18 if (arr[i] < v) { 19 std::swap(arr[i], arr[lt + 1]); // 如果当前位置元素<v,则将当前位置元素与=v部分的第一个元素交换位置 20 i++; // i++ 考虑下一个元素 21 lt++; // lt++ 表示<v部分多了一个元素 22 } 23 else if (arr[i] > v) { // 如果当前位置元素>v,则将当前位置元素与>v部分的第一个元素的前一个元素交换位置 24 std::swap(arr[i], arr[gt - 1]); // 此时i不用动,因为交换过来的元素还没有考虑他的大小 25 gt--; // gt-- 表示>v部分多了一个元素 26 } 27 else { // 如果当前位置元素=v 则只需要将i++即可,表示=v部分多了一个元素 28 i++; 29 } 30 } 31 32 std::swap(arr[left], arr[lt]); // 上面的遍历完成之后,将整个序列的第一个元素(也就是"基准"元素)放置到合适的位置 33 // 也就是将它放置在=v部分即可 34 __quickSort3Ways<T>(arr, left, lt - 1); // 对<v部分递归调用__quickSort3Ways函数进行三路排序 35 __quickSort3Ways<T>(arr, gt, right); // 对>v部分递归调用__quickSort3Ways函数进行三路排序 36 } 37 38 template<typename T> 39 void quickSort3Ways (T arr[], int count) 40 { 41 std::srand(std::time(NULL)); /* 种下随机种子 */ 42 __quickSort3Ways<T>(arr, 0, count - 1); /* 调用__quickSort3Ways函数进行三路快速排序 */ 43 } 44 /***********************************************************************************************/
3、性能测试
一般排序序列:
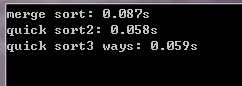
大量重复元素序列:
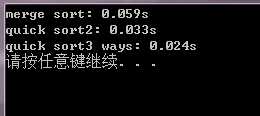
近乎有序状态的序列:
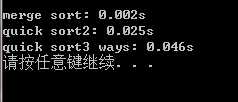
原文:http://www.cnblogs.com/deng-tao/p/6536302.html