softmax回归模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签$y$可以取两个以上的值,softmax回归是有监督的。
在logistic回归中,预测函数为:
$h_{\Theta}(x) = \frac{1}{1 + exp(-\Theta^Tx)}$
损失函数为
$J(\Theta) = - \frac{1}{m}[\sum^m_{i=1}y^{(i)}logh_{\Theta}(x^{(i)}) + (1 - y^{(i)})log(1 - h_{\Theta}(x^{i}))]$
在softmax回归中,我们解决的是多分类问题(相对于logistic回归解决的二分类问题),y可以取k个不同的值,我们想估计x的每一种分类结果出现的概率。对于给定的输入x,预测函数输出一个k维的向量来表示这k个估计的概率值。
预测函数为:
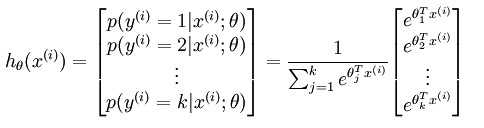
其中$\Theta_1,\Theta_2,...,\Theta_k$是模型的参数,$\frac{1}{\sum^k_{j=1}e^{\Theta^T_jx^{(i)}}}$对概率分布进行归一化,使得所有概率之和为1.
记 1{ 值为真的表达式 } = 1,1{ 值为假的表达式 } = 0.则softmax回归的损失函数为
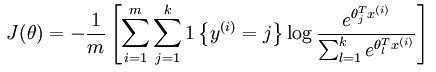
原文:http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/6542374.html