(a)
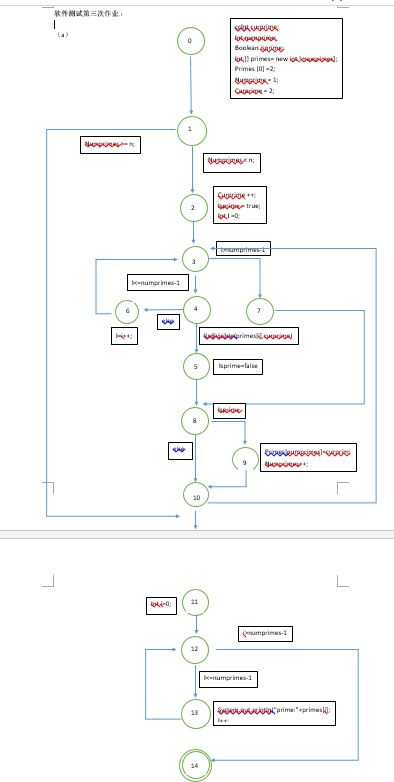
(b)
The difference of t1 ad t2 is n=4. If the code in line 24 is written as “isPrime = true” in miatake, t2 will be easy to find the fault.
(c)
In my understanding, this question is answered by a test case which does not execute the code in while loop. Which t(n=1).
(d)
Node cover:
{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14}
Edge cover:
{(0,1),(1,2),(2,3)(3,4),(4,6),(6,3),(3,7),(7,8),(4,5),(5,8),(8,9)(9,10),(8,10),(1,10),(10,3),(10,11),(11,12),(12,13),(12,14)}
Prime path cover:
{(0,1,2,3,4,5,8,9,10,11,12,14),(0,1,2,3,4,5,8,10,11,12,14),(0,1,2,3,4,5,8,9,10,11,12,13), (0,1,2,3,4,5,8,10,11,12,13),(0,1,2,3,7,8,9,10,11,12,14),(0,1,2,3,7,8,9,10,11,12,13),(0,1,2,3,7,8,10,11,12,13),(0,1,11,12,13),(0,1,11,12,14),(3,4,6,3),(3,7,8,9,10,3),(3,7,8,10,3),(3,4,5,8,9,10,3),(3,4,5,8,10,3),(12,13,12)}
Write a Prime-path-cover-test
The code of main.java:
package primes;
public class main {
public String printPrimes (int n)
{
int max=100;
int curPrime;
int numPrimes;
boolean isPrime;
String result = "";
int [] primes = new int [max];
primes [0] = 2;
numPrimes = 1;
curPrime = 2;
while (numPrimes < n)
{
curPrime++;
isPrime = true;
for (int i = 0; i <= numPrimes-1; i++)
{
if (curPrime%primes[i]==0)
{
isPrime = false;
break;
}
}
if (isPrime)
{
primes[numPrimes] = curPrime;
numPrimes++;
}
}
for (int i = 0; i <= numPrimes-1; i++)
{
result += primes[i]+" ";
}
return result;
}
}
The test code:
package primes;
import static org.junit.Assert.*;
import org.junit.After;
import org.junit.Before;
import org.junit.Test;
import primes.main;
public class mainTest {
main temp;
String xing;
@Before
public void setUp() throws Exception {
temp= new main();
}
@After
public void tearDown() throws Exception {
}
@Test
public void testPrintPrimes1() {
xing = temp.printPrimes(2);
assertEquals("2 3 ", xing);
}
@Test
public void testPrintPrimes2() {
xing = temp.printPrimes(3);
assertEquals("2 3 5 ", xing);
}
}
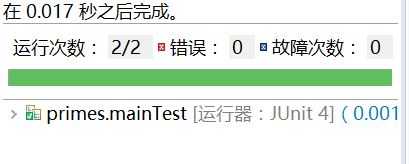
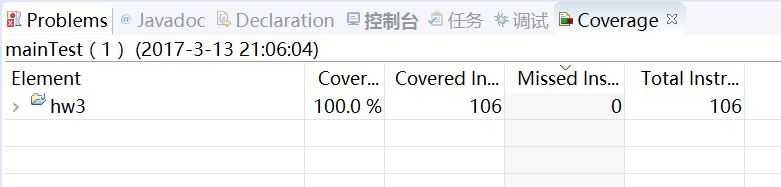
Result:
原文:http://www.cnblogs.com/jyc-blog/p/6545600.html