逻辑回归推导

1、主要内容

　　逻辑回归的推导，分别推导出y={0，1}和y = {-1， +1}，之前关于林轩田老师和李航老师关于逻辑回归的推导弄混了，林轩田老师的推导是建立在后面的—1， +1的分类，李航老师的是关于0， 1的推导。

2、关于逻辑斯蒂模型

　　逻辑斯蒂模型从逻辑斯蒂分布得到，这一部分见李航老师的《统计学习方法》。　

3、公式推导

　　两种推导都是采用对数似然最大方式进行模型的参数估计，不同之处就在于模型最后的映射结果不同，造成中间步骤关于0，1和 -1， 1的不同的处理，这个也是重点以后遇到相关的问题也可以采用类似的方式进行处理。同时将求最大似然函数取负号然后将求最大变成求最小值。

　　当训练数据为 x_i 对 y = {0， 1}的处理：

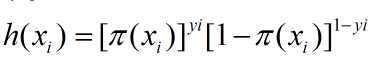
　　其中为逻辑斯蒂模型:

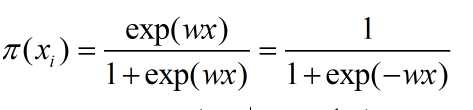
　　因此在整个训练数据上的似然函数就是：

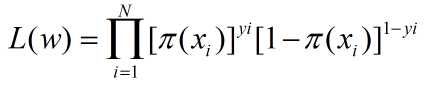
 　　对数似然函数为：

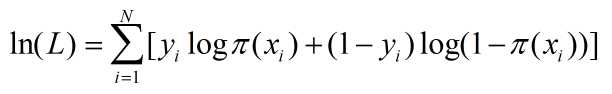
　　对其进一步的整理：

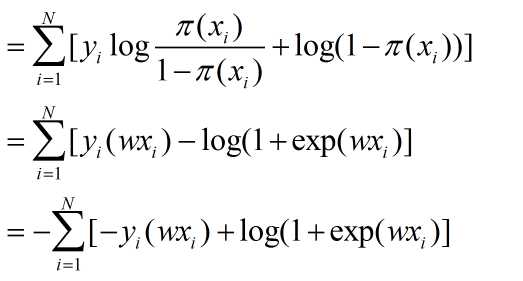
　　最后可以得到逻辑回顾的损失函数，同时在此处是求最大的似然估计，也就是求上面式子的最大值，添加符号将求最大变成最小值，然后对其求梯度：

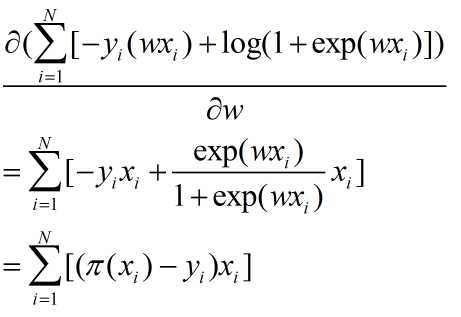
 　　对 y = {-1， +1}的处理：

　　观察逻辑斯蒂回归模型可以直到：

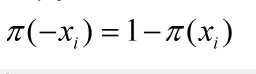
　　因此对于x_i来说：

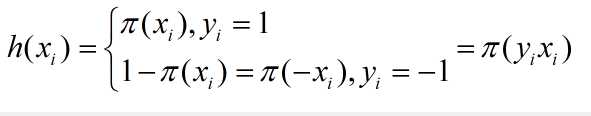
　　因此整个训练模型的似然函数为

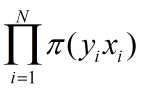
　　对数似然函数为：

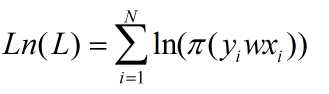
　　最后求似然函数的负数梯度可知：

逻辑回归推导

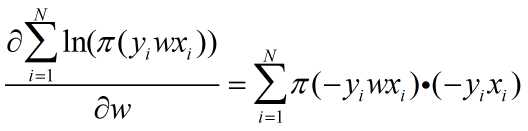
原文：http://www.cnblogs.com/daguankele/p/6549891.html