问题描述
给定n个矩阵A1,A2 ,...,An,相邻的矩阵是可乘的,如何确定一个最优计算次序,使得以此次序计算需要的数乘次数最少?
计算次序对计算性能的影响:
假设n=3,A1,A2,A3的维数分别为10×100,100×5,5×50。考察A1×A2×A3需要的数乘次数,有以下
两种计算方式:
(1)(A1×A2)×A3:10×100×5+10×5×50=7500
(2) A1×(A2×A3):100×5×50+10×100×50=75000
通过这个简单的例子足以说明,矩阵的计算次序对计算性能的影响极大。
分析:
1.最优解的结构
将矩阵乘积AiAi+1...Aj记为A[i:j],要求计算A[1:n]的最优计算次序,假设将这个矩阵链断开,分为两个子
矩阵链的乘积。也就是(AiAi+1...Ak)(Ak+1...Aj),先计算A[i:k]和A[k+1,j],然后将计算结果相乘得到A[i:j].
这样,A[i:j]的计算量就等于A[i:k]和A[k+1:j]的计算量与A[i:k]与A[k+1:j]两个矩阵相乘的计算量。
关键的一点是,如果找到了一种A[1:n]的最优计算次序,那么以这个次序计算A[1:k]与A[k+1:n]的也是
最优的。用反证法说明,如果有一个子数组不是最优的,那么可以找到使原问题最优的次序。
2.建立子问题与原问题解的联系
在计算得到子问题的解后,要想办法将子问题的解进行组合,以得到原问题的解。
假设A[i:j]在最优计算次序的情况下需要的乘法次数用m[i][j]来表示。在计算A[i:j]时,将矩阵链断开,
得到A[i:k]和A[k+1:j]两个矩阵链,分别计算出它们在最优次序下的乘法次数m[i][k]和m[k+1][j],然后加上
矩阵A[i:k]和A[k+1:j]相乘所需要的乘法次数。用向量p来表示矩阵的维度,矩阵Ai的维度是pi-1×pi。
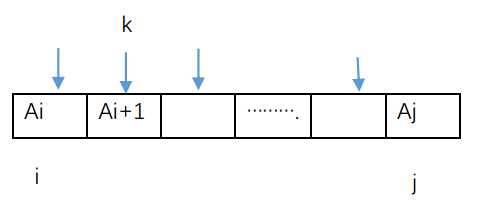
我们通过将矩阵链A[i:j]划分为较小的矩阵链A[i:k]和A[k+1:j]来计算A[i:j]的最优值,这样的划分方式如上图所示,
共有j-i种。
通过上面的分析,可以得到如下的递推关系
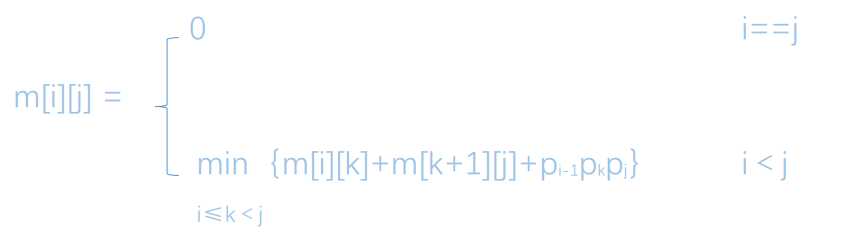
m[i][j]给出了最优值,即计算A[i:j]所需的最少乘法次数。同时,还确定了该最优次序对应的断开位置k:
m[i][j] = m[i][k] + m[k+1][j] + pi-1pkpj
将得到每个子矩阵链时的断开位置k记录下来,就可以构造出最优次序。
计算过程(以长度为4的矩阵链为例)
递归树如下:
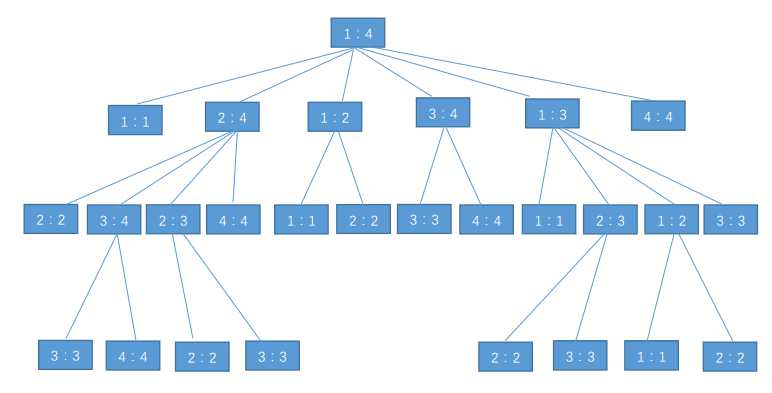
图中有边相连表示在计算上层结点时需要使用到下层子问题的结果进行组合,采用自底向上的方法,先计算简单子问题的结果,再
利用递推关系式最终得到原问题的结果。
部分代码
1.寻找最优次序
static void matrix_chain(int *dim,int **m,int **s,int n) { for(int i=1;i<=n;i++) m[i][i]=0; for(int r=2;r<=n;r++) for(int i=1;i<=n-r+1;i++){ int j=r+i-1; m[i][j]=m[i+1][j]+dim[i-1]*dim[i]*dim[j]; s[i][j]=i; for(int k=i+1;k<j;k++){ int t=m[i][k]+m[k+1][j]+dim[i-1]*dim[k]*dim[j]; if(t<m[i][j]){ m[i][j] = t; s[i][j] = k; } } } }
用n+1维向量dim来表示n个矩阵的维度,用矩阵m来保存计算子问题时得到的子问题的最优解,以减少计算次数,矩阵s用来保存每个子问题的最优断开位置k
2.用保存的数组s来构造最优次序
void trace_back(int **s,int start,int end) { if(start == end) return; trace_back(s,start,s[start][end]); trace_back(s,s[start][end]+1,end); printf("A(%d,%d)xA(%d,%d)\n",start,s[start][end],s[start][end]+1,end); }
原文:http://www.cnblogs.com/zclm/p/6551325.html