如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入格式:
第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
输出格式:
一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
0 2 4 3
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=15
对于40%的数据:N<=100,M<=10000
对于70%的数据:N<=1000,M<=100000
对于100%的数据:N<=10000,M<=500000
样例说明:
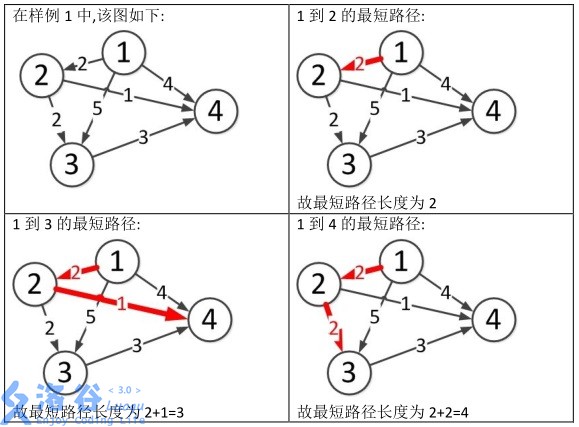
明天要市赛了,复习一些模板。
1 program rrr(input,output); 2 const 3 inf=123456789; 4 type 5 etype=record 6 t,w,next:longint; 7 end; 8 var 9 e:array[0..500050]of etype; 10 a,q,dis:array[0..10010]of longint; 11 inq:array[0..10010]of boolean; 12 n,m,s,i,h,t,u,v,w,cnt:longint; 13 procedure add(u,v,w:longint); 14 begin 15 inc(cnt);e[cnt].t:=v;e[cnt].w:=w;e[cnt].next:=a[u];a[u]:=cnt; 16 end; 17 begin 18 assign(input,‘r.in‘);assign(output,‘r.out‘);reset(input);rewrite(output); 19 readln(n,m,s); 20 fillchar(a,sizeof(a),0); 21 for i:=1 to m do begin read(u,v,w);add(u,v,w); end; 22 fillchar(inq,sizeof(inq),false); 23 for i:=1 to n do dis[i]:=inf; 24 h:=0;t:=1;q[1]:=s;dis[s]:=0;inq[s]:=true; 25 while h<>t do 26 begin 27 inc(h);if h>10000 then h:=1; 28 i:=a[q[h]]; 29 while i<>0 do 30 begin 31 if dis[q[h]]+e[i].w<dis[e[i].t] then 32 begin 33 dis[e[i].t]:=dis[q[h]]+e[i].w; 34 if not inq[e[i].t] then 35 begin 36 inq[e[i].t]:=true; 37 inc(t);if t>10000 then t:=1;q[t]:=e[i].t; 38 end; 39 end; 40 i:=e[i].next; 41 end; 42 inq[q[h]]:=false; 43 end; 44 for i:=1 to n do if dis[i]=inf then write(maxlongint,‘ ‘) else write(dis[i],‘ ‘); 45 close(input);close(output); 46 end.
原文:http://www.cnblogs.com/Currier/p/6568978.html