【SinGuLaRiTy-1010】Copyrights (c) SinGuLaRiTy 2017. All Rights Reserved.
Some Method Are Reprinted From 杨思雨-《伸展树的基本操作与应用》
二叉查找树（Binary Search Tree）能够支持多种动态集合操作。因此，在信息学竞赛中，二叉排序树起着非常重要的作用，它可以被用来表示有序集合、建立索引或优先队列等。作用于二叉查找树上的基本操作的时间是与树的高度成正比的。对一个含 n各节点的完全二叉树，这些操作的最坏情况运行时间为 O(log n)。但如果树是含n 个节点的线性链，则这些操作的最坏情况运行时间为 O(n)。而有些二叉查找树的变形，其基本操作在最坏情况下性能依然很好，比如红黑树、AVL 树等等。本文将要介绍的伸展树（Splay Tree），也是对二叉查找树的一种改进，虽然它并不能保证树一直是“平衡”的，但对于伸展树的一系列操作，我们可以证明其每一步操作的平摊复杂度都是 O(log n)。所以从某种意义上说，伸展树也是一种平衡的二叉查找树。而在各种树状数据结构中，伸展树的空间要求与编程复杂度也都是很优秀的。
伸展树是二叉查找树的一种改进，与二叉查找树一样，伸展树也具有有序性。即伸展树中的每一个节点 x 都满足：该节点左子树中的每一个元素都小于 x，而其右子树中的每一个元素都大于 x。与普通二叉查找树不同的是，伸展树可以自我调整，这就要依靠伸展操作 Splay(x,S)。
情况一：节点 x 的父节点 y 是根节点。这时，如果 x 是 y 的左孩子，我们进行一次 Zig（右旋）操作；如果 x 是 y 的右孩子，则我们进行一次 Zag（左旋）操作。经过旋转，x 成为二叉查找树 S 的根节点，调整结束。如图 1 所示
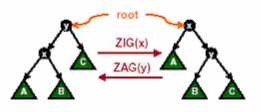图 1
情况二：节点 x 的父节点 y 不是根节点，y 的父节点为 z，且 x 与 y 同时是各自父节点的左孩子或者同时是各自父节点的右孩子。这时，我们进行一次Zig-Zig 操作或者 Zag-Zag 操作。如图 2 所示
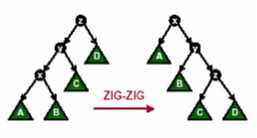图 2
情况三：节点 x 的父节点 y 不是根节点，y 的父节点为 z，x 与 y 中一个是其父节点的左孩子而另一个是其父节点的右孩子。这时，我们进行一次 Zig-Zag 操作或者 Zag-Zig 操作。如图 3 所示
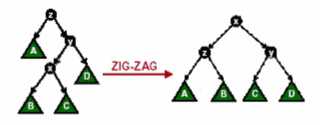图 3
如图 4 所示，执行 Splay(1,S)，我们将元素 1 调整到了伸展树 S 的根部。再执行 Splay(2,S)，如图 5 所示，我们从直观上可以看出在经过调整后，伸展树比原来“平衡”了许多。而伸展操作的过程并不复杂，只需要根据情况进行旋转就可以了，而三种旋转都是由基本得左旋和右旋组成的，实现较为简单。
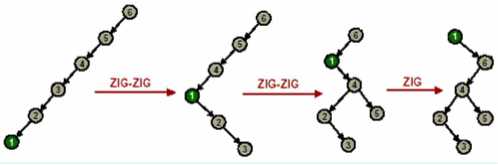图 4 Splay(1,S)
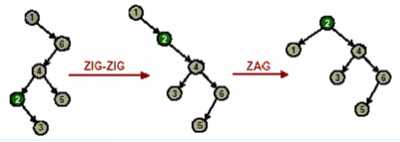图 5 Splay(2,S)
利用 Splay 操作，我们可以在伸展树 S 上进行如下运算：
Find(x,S)：判断元素 x 是否在伸展树 S 表示的有序集中。首先，与在二叉查找树中的查找操作一样，在伸展树中查找元素 x。如果 x在树中，则再执行 Splay(x,S)调整伸展树。
int find(int now,int val){//pos
if(mx[son[now][0]]>=val)return find(son[now][0],val);
if(key[now]==val)return now;
if(mi[son[now][1]]<=val)return find(son[now][1],val);
return now;
}
int rank(int now,int val){
if(key[now]==val)return size[son[now][0]]+1;
else if(val<key[now])return rank(son[now][0],val);
else if(val>key[now])return size[son[now][0]]+1+rank(son[now][1],val);
}
int kth(int now,int th){
if(size[son[now][0]]+1==th)return now;
else if(size[son[now][0]]+1>th)return kth(son[now][0],th);
else return kth(son[now][1],th-size[son[now][0]]-1);
}
int pre(int val){
int tmp=kth(son[val][0],size[son[val][0]]);
splay(tmp,val);
return key[tmp];
}
int succ(int val){
int tmp=kth(son[val][1],1);
splay(tmp,val);
return key[tmp];
}
也与处理普通的二叉查找树一样，将 x 插入到伸展树 S 中的相应位置上，再执行 Splay(x,S)。
首先，找到一个合适的位置
int getpos(int now,int val){
if((key[now]<val)&&(size[son[now][1]]))return getpos(son[now][1],val);
else if((key[now]>val)&&(size[son[now][0]]))return getpos(son[now][0],val);
return now;
}
但是我们并不能保证这个点是大于还是小于插入节点
void insert(int root,int pos,int val){
int sroot=father[root];
splay(root=getpos(root,val),sroot);
if(key[root]<val){
succ(root);//十分重要
rotate(root=son[root][1]);
}
int tmp=son[root][0];key[pos]=val;
son[root][0]=pos;father[pos]=root;
son[pos][0]=tmp;father[tmp]=pos;
updata(pos);updata(root);
splay(pos,0);
}
我们把刚好比插入点大的点作为根，在左子树插入。如果根小于插入点，则要将根的后继变成根（！！！注意不是根的右儿子！！！）
将元素 x 从伸展树 S 所表示的有序集中删除。首先，用在二叉查找树中查找元素的方法找到 x 的位置。如果 x 没有孩子或只有一个孩子，那么直接将 x 删去，并通过 Splay 操作，将 x 节点的父节点调整到伸展树的根节点处。否则，则向下查找 x 的后继 y，用 y 替代 x 的位置，最后执行 Splay(y,S)，将 y 调整为伸展树的根。
void dele(int root,int val){
int sroot=father[root];
splay(root=find(root,val),sroot);
if(son[root][1])splay(succ(root),root);
son[sroot][flag(root)]=son[root][1];
father[son[root][1]]=sroot;
son[son[root][1]][0]=son[root][0];
father[son[root][0]]=son[root][1];
updata(son[root][1]);
}
将两个伸展树 S1 与 S2 合并成为一个伸展树。其中 S1 的所有元素都小于 S2 的所有元素。
首先，我们找到伸展树 S1 中最大的一个元素 x，再通过 Splay(x,S1)将 x 调整到伸展树 S1 的根。然后再将 S2 作为 x 节点的右子树。这样，就得到了新的伸展树 S。如图 6 所示
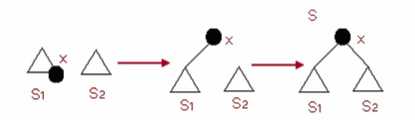图 6
(个人觉得这个操作运用的比较少)
以 x 为界，将伸展树 S 分离为两棵伸展树 S1 和 S2，其中 S1中所有元素都小于 x，S2 中的所有元素都大于 x。首先执行 Find(x,S)，将元素 x 调整为伸展树的根节点，则 x 的左子树就是S1，而右子树为 S2。如图 7 所示
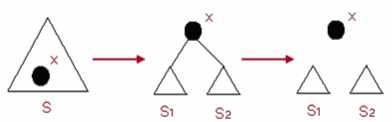图 7
splay是基本操作，rotate是splay的基本操作。splay(now,root)把now splay到root的下面。单旋和双旋就不说了。我们可以简化操作，如果是一字型（方向相同）则先旋father，否则先旋now。然后再旋now。
可将一字型与之字形的情况合并：
void splay(int now,int root){
while(father[now]!=root){
if(father[father[now]]!=root){
if(flag(now)==flag(father[now]))rotate(father[now]);
else rotate(now);
}
rotate(now);
}
}
rotate now是指将now绕father rotate。有两个方向，表示now是father的左儿子还是右儿子。
bool flag(int now){
return son[father[now]][1]==now;
}
通过方向标记，我们可以将两个方向的rotate合成一个：
void rotate(int now){
int fa=father[now],fx=flag(now);
son[fa][fx]=son[now][!fx];
if(son[now][!fx])father[son[now][!fx]]=fa;
//连接father和son[now]
son[father[fa]][flag(fa)]=now;
father[now]=father[fa];
//连接grandpa和now
son[now][!fx]=fa;
father[fa]=now;
//连接now和father
updata(fa);updata(now);
}
别忘了rotate完成后要updata：
void updata(int pos){
size[pos]=size[son[pos][0]]+size[son[pos][1]]+1;
}
这里还有另一个标准版本的Splay操作：
void splay(int x,int goal)
{
for(int y;(y=fa[x])!=goal;rotate(x))
{
int z;
if((z=fa[y])!=goal)
{
if((ch[z][1]==y)==(ch[y][1]==x))
rotate(y);
else rotate(x);
}
}
if(goal==0)root=x;
}
void rotate(int x)
{
if(x==0||fa[x]==0)return;
int y=fa[x],z=fa[y];
bool flag=(ch[y][1]==x);
ch[y][flag]=ch[x][!flag];
if(ch[x][!flag])fa[ch[x][!flag]]=y;
ch[x][!flag]=y;
fa[y]=x;
fa[x]=z;
if(z)ch[z][ch[z][1]==y]=x;
}
int insert(int &r,int x,int f)
{
int temp1,temp2;
if(r==0)
{
sale[++tot]=x;
r=tot;
fa[r]=f;
splay(r,0);
return INF;
}
if(x==sale[r])
return 0;
else if(x<sale[r])
{
temp1=sale[r]-x;
temp2=insert(ch[r][0],x,r);
return min(temp1,temp2);
}
else
{temp1=x-sale[r];
temp2=insert(ch[r][1],x,r);
return min(temp1,temp2);
}
}
由以上这些操作的实现过程可以看出，它们的时间效率完全取决于 Splay 操作的时间复杂度。下面，我们就用会计方法来分析 Splay 操作的平摊复杂度。首先，我们定义一些符号：S(x)表示以节点 x 为根的子树。|S|表示伸展树 S的节点个数。令μ(S) = [ log|S| ]，μ(x)=μ(S(x))。如图 8 所示
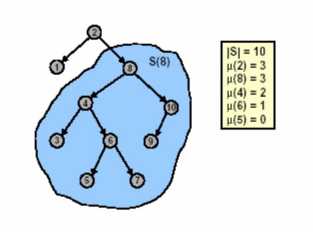图 8
我们用 1 元钱表示单位代价（这里我们将对于某个点访问和旋转看作一个单位时间的代价）。定义伸展树不变量：在任意时刻，伸展树中的任意节点 x 都至少有μ(x)元的存款。
在 Splay 调整过程中，费用将会用在以下两个方面：
(1)为使用的时间付费。也就是每一次单位时间的操作，我们要支付 1 元钱。
(2)当伸展树的形状调整时，我们需要加入一些钱或者重新分配原来树中每个节点的存款，以保持不变量继续成立。
下面我们给出关于 Splay 操作花费的定理：
每一次Splay(x,S)操作中，调整树的结构与保持伸展树不变量的总花费不超过3u(S)+1.
证明：用μ(x)和μ’(x)分别表示在进行一次 Zig、Zig-Zig 或 Zig-Zag 操作前后节点 x 处的存款。
下面我们分三种情况分析旋转操作的花费：
情况一：如图 9 所示
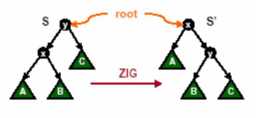图 9
我们进行 Zig 或者 Zag 操作时，为了保持伸展树不变量继续成立，我们需要花费：
μ’(x) +μ’(y) -μ(x) -μ(y) = μ’(y) -μ(x)
≤ μ’(x) -μ(x)
≤ 3(μ’(x) -μ(x))
=3(μ(S) -μ(x))
此外我们花费另外 1 元钱用来支付访问、旋转的基本操作。因此，一次 Zig 或 Zag 操作的花费至多为 3(μ(S) -μ(x))。
情况二：如图 10 所示
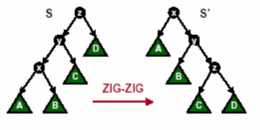图 10
我们进行 Zig-Zig 操作时，为了保持伸展树不变量，我们需要花费：
μ’(x) +μ’(y) +μ’(z) -μ(x) -μ(y) -μ(z) = μ’(y) +μ’(z) -μ(x) -μ(y)
=(μ’(y) -μ(x)) + (μ’(z) -μ(y))
≤ (μ’(x) -μ(x)) + (μ’(x) -μ(x))
=2 (μ’(x) -μ(x))
与上种情况一样，我们也需要花费另外的 1 元钱来支付单位时间的操作。
当μ’(x) <μ(x) 时，显然 2 (μ’(x) -μ(x)) +1 ≤ 3 (μ’(x) -μ(x))。也就是进行Zig-Zig 操作的花费不超过 3 (μ’(x) -μ(x))。
当μ’(x) =μ(x) 时，我们可以证明μ’(x) +μ’(y) + μ’(z) <μ(x) +μ(y) +μ(z)，也就是说我们不需要任何花费保持伸展树不变量，并且可以得到退回来的钱，用其中的 1 元支付访问、旋转等操作的费用。为了证明这一点，我们假设μ’(x) +μ’(y)+ μ’(z) >μ(x) +μ(y) +μ(z)。
联系图 9，我们有μ(x) =μ’(x) =μ(z)。那么，显然μ(x) =μ(y) =μ(z)。于是，可以得出μ(x) =μ’(z) =μ(z)。令 a = 1 + |A| + |B|，b = 1 + |C| + |D|，那么就有
[log a] = [log b] = [log (a+b+1)] ①
我们不妨设 b≥a，则有
[log (a+b+1)] ≥ [log (2a)]
= 1+[log a]
> [log a] ②
①与②矛盾，所以我们可以得到μ’(x) =μ(x) 时，Zig-Zig 操作不需要任何花费，显然也不超过 3 (μ’(x) -μ(x))。
情况三：与情况二类似，我们可以证明，每次 Zig-Zag 操作的花费也不超过3 (μ’(x) -μ(x))。
以上三种情况说明，Zig 操作花费最多为 3(μ(S)-μ(x))+1，Zig-Zig 或 Zig-Zag操作最多花费 3(μ’(x)-μ(x))。那么将旋转操作的花费依次累加，则一次 Splay(x,S)操作的费用就不会超过 3μ(S)+1。也就是说对于伸展树的各种以 Splay 操作为基础的基本操作的平摊复杂度，都是 O(log n)。所以说，伸展树是一种时间效率非常优秀的数据结构。
由上面的分析介绍，我们可以发现伸展树有以下几个优点：
(1)时间复杂度低，伸展树的各种基本操作的平摊复杂度都是 O(log n)的。在树状数据结构中，无疑是非常优秀的。
(2)空间要求不高。与红黑树需要记录每个节点的颜色、AVL 树需要记录平衡因子不同，伸展树不需要记录任何信息以保持树的平衡。
(3)算法简单，编程容易。伸展树的基本操作都是以 Splay 操作为基础的，而Splay 操作中只需根据当前节点的位置进行旋转操作即可。虽然伸展树算法与 AVL 树在时间复杂度上相差不多，甚至有时候会比 AVL树慢一些，但伸展树的编程复杂度大大低于 AVL 树。在竞赛中，使用伸展树在编程和调试中都更有优势。
| 顺序查找 | 线段树 | AVL树 | 伸展树 | |
| 时间复杂度 | O(n^2) | O(nlog a) | O(nlog n) | O(nlog n) |
| 空间复杂度 | O(n) | O(a) | O(n) | O(n) |
| 编程复杂度 | 简单 | 较简单 | 复杂 | 较简单 |
都是一些模板题，适合练练手。
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=3e5+111;
int data[N],num[N],t[N][2],id,fa[N];
int flip[N],root,f;
void pushup(int x)
{
num[x]=num[t[x][0]]+num[t[x][1]]+1;
}
void pushdown(int x)
{
if(flip[x])
{
flip[x]=0;
flip[t[x][0]]^=1;
flip[t[x][1]]^=1;
swap(t[x][0],t[x][1]);
}
}
void Rotate(int x,int w)
{
int y=fa[x];
int z=fa[y];
pushdown(y);
t[y][!w]=t[x][w];
fa[t[x][w]]=y;
t[z][t[z][1]==y]=x;
fa[x]=z;
t[x][w]=y;
fa[y]=x;
pushup(y);
}
void newnode(int &x,int y,int v)
{
x=++id;
t[x][0]=t[x][1]=0;
fa[x]=y;
data[x]=v,flip[x]=0;
num[x]=1;
}
void build(int &x,int y,int l,int r)
{
if(l<=r)
{
int mid=(l+r)>>1;
newnode(x,y,mid);
build(t[x][0],x,l,mid-1);
build(t[x][1],x,mid+1,r);
pushup(x);
}
}
void init(int n)
{
f=id=root=0;
t[0][0]=t[0][1]=num[0]=data[0]=flip[0]=fa[0]=0;
newnode(root,0,-1);
newnode(t[1][1],root,-1);
build(t[t[1][1]][0],t[1][1],1,n);
pushup(t[1][1]);
pushup(1);
}
void Splay(int x,int y)
{
if(x!=y)
{
pushdown(x);
while(fa[x]!=y)
{
if(t[fa[x]][0]==x)
Rotate(x,1);
else
Rotate(x,0);
}
pushup(x);
if(!y)
root=x;
}
}
int Kth(int k)
{
int x=root;
pushdown(root);
for(;num[t[x][0]]+1!=k;)
{
if(num[t[x][0]]+1>k)
x=t[x][0];
else
k-=num[t[x][0]]+1,x=t[x][1];
pushdown(x);
}
return x;
}
void Flip(int a,int b)
{
a=Kth(a);
b=Kth(b+2);
Splay(a,0);
Splay(b,a);
flip[t[b][0]]^=1;
}
void Cut(int a,int b,int c)
{
int tmp,d;
a=Kth(a);b=Kth(b+2);
Splay(a,0);Splay(b,a);
tmp=t[b][0];t[b][0]=0;
pushup(b);pushup(a);
d=Kth(c+2);c=Kth(c+1);
Splay(c,0);Splay(d,c);
t[d][0]=tmp;fa[tmp]=d;
pushup(d);pushup(c);
}
void Inorder(int x)
{
if(x)
{
pushdown(x);
Inorder(t[x][0]);
if(data[x]>0)
{
if(f)
putchar(‘ ‘);
else
f=1;
printf("%d",data[x]);
}
Inorder(t[x][1]);
}
}
int main()
{
int n,m;
char op[9];
while(scanf("%d%d",&n,&m)!=EOF)
{
if(n==-1)
break;
init(n);
int a,b,c;
while(m--){
scanf("%s",op);
if(op[0]==‘F‘)
{
scanf("%d%d",&a,&b);
Flip(a,b);
}
else
{
scanf("%d%d%d",&a,&b,&c);
Cut(a,b,c);
}
}
Inorder(root);
puts("");
}
return 0;
}
第一行为正整数 ，表示该公司从成立一直到现在的天数
接下来的n行每行有一个整数(一定有数据小于〇) ，表示第i天公司的营业额。
输出文件仅有一个正整数，即每一天的最小波动值之和。答案保证在int范围内。
6
5
1
2
5
4
6
12
结果说明：5+|1-5|+|2-1|+|5-5|+|4-5|+|6-5|=5+4+1+0+1+1=12
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define MAXN 100005
#define INF 10000000
int ch[MAXN][2],fa[MAXN],sale[MAXN];
int ans,tot,root;
#define min(a,b) ((a)>(b)?(b):(a))
void rotato(int x)
{
if(x==0||fa[x]==0)return;
int y=fa[x],z=fa[y];
bool flag=(ch[y][1]==x);
ch[y][flag]=ch[x][!flag];
if(ch[x][!flag])fa[ch[x][!flag]]=y;
ch[x][!flag]=y;
fa[y]=x;
fa[x]=z;
if(z)ch[z][ch[z][1]==y]=x;
}
void splay(int x,int goal)
{
for(int y;(y=fa[x])!=goal;rotato(x))
{
int z;
if((z=fa[y])!=goal)
{
if((ch[z][1]==y)==(ch[y][1]==x))
rotato(y);
else rotato(x);
}
}
if(goal==0)root=x;
}
int insert(int &r,int x,int f)
{
int temp1,temp2;
if(r==0)
{
sale[++tot]=x;
r=tot;
fa[r]=f;
splay(r,0);
return INF;
}
if(x==sale[r])
return 0;
else if(x<sale[r])
{
temp1=sale[r]-x;
temp2=insert(ch[r][0],x,r);
return min(temp1,temp2);
}
else
{temp1=x-sale[r];
temp2=insert(ch[r][1],x,r);
return min(temp1,temp2);
}
}
int main()
{
int n,t;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&t);
if(i)ans+=insert(root,t,0);
else {ans=t;
insert(root,t,0);
}
}
printf("%d\n",ans);
}
Time： 2017-03-22
原文：http://www.cnblogs.com/SinGuLaRiTy2001/p/6602276.html