【SinGuLaRiTy-1008】 Copyright (c) SinGuLaRiTy 2017. All Rights Reserved.
对于所有的题目:Time Limit:1s | Memory:256 MB
大家都知道28定律吧,据说世界上20%的人拥有80%的财富。现在你对一家银行的账户进行检测,看是否符合28定律,或者有更强的定律。比如说,10%的人拥有85%的财富。更准确的描述是:对N个银行账户进行调查,你的任务是找出两个数A,B,使得B-A的差最大。A,B的含义是A%的人拥有B%的财富。(Special Judge)
输入的第一行包含一个整数N(1<=N<=300000),表示银行账户的个数。
接下来一行包含N个整数,每个整数在区间[0,100000000],表示这N个账户中的存款金额。
输出两行,分别是两个实数A,B。A,B的含义如题所述。误差在0.01内可以接受。
| 样例输入 | 样例输出 |
|
2 100 200 |
50.0 66.66666666666666 |
Paret’s principle, also known as the “80/20 rule”, states that in many situations 80% of results come from 20% of (the most important) causes. For instance, Microsoft found that, by fixing 20% of most commonly reported bugs, they would eliminate 80% of downtime in their systems. In the business world, it is often said that 80% of income comes from 20% of the most important clients. In the world of mobile games, when it comes to games with free basic functionality, 50% of profit comes from 0.5% of players. Some say that 80% of your success will come from 20% of your activities. It is a known fact that 80% of the world’s goods is owned by 20% of (the richest) people.
Your task is to check the validity of this rule based on the bank accounts owned by clients of a single bank. Is it true that 20% of accounts hold 80% of the total money? Does a stronger claim hold, for instance, that only 10% of accounts hold 85% of the total money?
More precisely: based on the given account balances of N bank clients, your task is to find numbers ?A and ?B with the maximal difference ?B - A such that we can say that precisely A% of accounts hold B% of the total money of all clients of the bank.
The first line of input contains the integer N (1 ≤ N ≤ 300 000), the number of clients in the bank.
The following line contains N integers from the interval [0, 100 000 000], the balances of bank accounts in euros.
In two lines, you must output two real numbers from the task, A and B, omitting the percentage sign. Solution with the greatest B - A difference will be unique. A deviation from the official solution for less than 0.01 will be tolerated.
给你N个矩形,这些矩形在平面坐标系中,并且以坐标系的零点为中心,它们的边都平行于坐标轴。每个矩形由宽度和高度可以唯一确定。现在对矩形进行染色操作。下图即是样例的示意图:
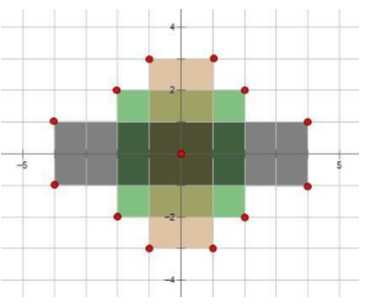
现在请你计算有染色区域的面积。
第一行包含1个整数N(1<=n<=1000000),表示矩形的个数。
接下来N行包含两个偶数X和Y(2<=X,Y<=10000000),分别表示宽度和高度。
唯一的一行,表示区域面积。
|
样例输入 |
样例输出 |
|
3 8 2 4 4 2 6 |
28 |
You are given N rectangles, which are centered in the center of the Cartesian coordinate system and their sides are parallel to the coordinate axes. Each rectangle is uniquely identified with its width (along the x-axis) and height (along the y-axis). The lower image depicts the first sample test.

Mirko has coloured each rectangle in a certain color and now wants to know the area of the coloured part of the paper. In other words, he wants to know the number of unit squares that belong to at least one rectangle.
The first line of input contains the integer N (1 ≤ N ≤ 1 000 000), the number of rectangles.
Each of the following N lines contains even integers X and Y (2 ≤ X, Y ≤ 107), dimensions (width and height, respectively) of the corresponding rectangles.
The first and only line of output must contain the required area.
In test cases worth 40% of total points, all numbers from the input will be smaller than 3333.
In test cases worth 50% of total points, not a single rectangle will be located strictly within another rectangle.
有N个城市,它们之间都有双向的航线。一个疯狂的航空公司老板经常改变航班日程。每天他都会做以下的事情:
1.选择一个城市
2.从该城市出发没有航线到达的城市全部开通航线,同时将之前开通的从该城市出发的所有航线全部取消
举个例子,比如从城市5出发,可以达到城市1和城市2,不能到达城市3和城市4,老板选择城市5做出改变后,那么城市5就有航班可以到达城市3和城市4,同时没有航班到达城市1和城市2了。
市民们想知道有没有一天,航线形成一个完全图。即每一个城市都有到达其他所有城市的航线,或者永远不可能形成一个完全图,不管老板如何操作。写一个程序来判断
第一行包含一个整数N(2<=N<=1000),表示城市的数量。城市的编号从1到N
第二行包含一个整数M(0<=M<=N*(N-1)/2),表示当前航班的数量。
接下来又M行,每行包含两个不同的整数,A,B,表示A,B两个城市有航线。
有且只有一行,如果能够形成完全图,则输出DA,如果不能形成完全图,则输出NE
|
样例输入 |
样例输出 |
|
3 2 1 2 2 3 |
NE |
There are N cities in one country that are connected with two-way air links. One crazy airline president, Ronald Krump, often changes the flight schedule. More precisely, every day he does the following:
● chooses one of the cities,
● introduces flights from that city towards all other cities where these flights do not
currently exist, and at the same time cancels all existing flights from that city
For instance, if from city 5 flights exist towards cities 1 and 2, but not towards cities 3 and 4, after Krump’s change, there will exist flights from city 5 towards cities 3 and 4, but not towards cities 1 and 2.
The citizens of this country are wondering if a day could come when the flight schedule will be complete. In other words, when between each two different cities a (direct) flight will exist.
Write a programme that will, based on the current flight schedule, determine whether it is possible to have a Complete Day, or whether this will never happen, no matter what moves Krump makes.
The first line of input contains the integer N (2 ≤ N ≤ 1000), the number of cities. The cities are labeled with numbers from 1 to N.
The second line contains the integer M (0 ≤ M < N*(N-1)/2), the number of current flights. Each of the following M lines contains two different numbers, the labels of the cities that are currently connected.
The first and only line of output must contain DA (Croatian for “yes”) or NE (Croatian for “no”).
Mirko是一个非常单纯的人,他的好朋友给他一个有N个自然数的数组,然后对他进行Q次查询.
每一次查询包含两个正整数L,R,表示一个数组中的一个区间[L,R],Mirko需要回答在这个区间中有多少个值刚好出现2次。
第一行包含两个整数N和Q(1<=N,Q<=500000)
第二行包含N个自然数,这些数均小于1000000000,表示数组中的元素。
接下来有Q行,每行包含两个整数L和R(1<=L<=R<=N)。
输出包含Q行,每行包含一次查询的答案。
|
样例输入 |
样例输出 |
|
5 2 1 1 1 1 1 2 4 2 3 |
0 1 |
Little Mirko is a very simple man. Mirko’s friend Darko has given him an array of N natural integers and asked him Q queries about the array that Mirko must answer.
Each query consists of two integers, the positions of the left and right end of an interval in the array. The answer to the query is the number of different values that appear exactly twice in the given interval.
The first line of input contains the integers N and Q (1 ≤ N, Q ≤ 500 000).
The second line of input contains N natural integers less than 1 000 000 000, the elements of the array.
Each of the following Q lines contains two integers, L and R (1 ≤ L ≤ R ≤ N), from the task.
The output must consist of Q lines, each line containing the answer to a query, respectively.
In test cases worth 56 points in total, the numbers N and Q will not be larger than 5000.
We will sort the amounts descendingly by size, from the largest to the smallest one. For each “prefix” that consists of K richest clients, we will calculate the corresponding numbers A and B, the share of that prefix in the number of accounts (A = K / N * 100%) and the total share of the money for that prefix: B = (the sum of K largest amounts) / (the sum of all amounts) * 100%. We now check if the difference B - A is the largest so far: if it is, we update the temporary variables A?_best,?B_best, the ones we ouput in the end.
Given the size of the array, we need to efficiently sort it, in the complexity O(N log N), and then efficiently calculate the sum of prefixes. The easiest way to do so is to calculate the sum of K-prefix by adding the K th element to the previously calculated (K-1)-prefix.
Necessary skills:?sorting
Category:?ad-hoc
It is enough to observe only the right half of the image and in the end double the result. The solution is to sum the heights of X-columns for X = 1, 2, …, 10^7, which can be done using a for loop.
How to determine the height of the column at coordinate X? It is larger than or equal to the height of column at coordinate X + 1. It is larger if a rectangle exists that ends at coordinate X and is higher than the column at coordinate X + 1, otherwise it is equal. Therefore, initially, we need to store the X-coordinates where the given rectangles end and their heights, then traverse the X-columns “backwards”, towards the beginning, in order to apply the aforementioned formula.
Necessary skills:?arrays
Category:?ad-hoc
For any line A-B we deduce: each Krump’s selection of city A or city B changes its existence,so its final existence depends only on the parity of the number of selections of cities A and B.Given this fact, it is sufficient to assume that Krump selects each city zero or one time(selection or non-selection), which greatly simplifies the task.We investigate two options: Krump either selects city 1, or he doesn’t. For each of the possibilities, we will check whether they can lead to a complete graph. If we’ve fixed the selection (or non-selection) of city 1, for each other city K we can easily determine if it needs to be selected, considering the parity that must enable the existence of flight route 1-K. This way, we determine the selections or non-selections of all cities from 2 to N. Since we’ve only ensured the existence of flight routes 1-K, we will check the existence of all other lines, and if all of them exist, the answer is DA (Croatian for “yes”). An alternative solution is the following: the answer is DA (Croatian for “yes”) if and only if the initial graph consists of exactly two components, each of them being a complete graph (clique). The proof is left as an exercise for the reader.
Necessary skills:?analytical reasoning
Category:?graphs
We will solve the task using the offline method, where we first input all queries, and then process them. To begin with, let’s define two functions, left(x), right(x) that correspond to the position of the first left and the first right element, respectively, of the same value as the one at position x. These two functions are easily computed, traversing from left to right, or from right to left, keeping track of the ‘latest’ of each value using a hash map, structure Map in C++ or a normal matrix, if we first compress the values. Let’s observe a query [L, R] and functions left(x), right(x). It is easily noticed that we will count in a position x for query [L, R] if left(x) < L <= x <= right(x) <= R < right(right(x)). Using natural language: we want the first left appearance of the value to be before the left end of the interval, and the first right appearance before or at the right end of the interval, in addition that there is no other occurrence of the value in the interval. With this, we ensure the counting of each pair of two identical values exactly once. Now the task is reduced to the following problem: for an x increment by 1 the solution of each query where left(x) < L <=left(left(x)) and where right(x) <= R < right(right(x )).
In order to execute this query, we need to construct a tournament data structure over allintervals in the following way: for each node of the tournament that covers interval [A, B], we need to ‘insert’ the query [L, R] if A <= L <= R, in other words, L e [A, B]. After this, for each x, we need to insert the interval right(x),right(right(x))> into all nodes of the tree of the interval <left(x),which is made of (typical query or update operation in a tournament data structure). There are O(lg N) such nodes for each x. After inserting queries and intervals into x), right(right(x))> into all nodes of the tree of which the tournament, we need to calculate the ‘contribution’ of each node to the queries located in that node. We perform this using the sweep technique and leave the implementation details as an exercise for the reader.The total complexity of the given solution is O(N lg?N). A solution of the complexity O(N lg2N) also exists, and is also left as an exercise for the reader.
Necessary skills:?sweep, data structures
Category:?tournament, data structures
[SinGuLaRiTy] COCI 2016~2017 #5
原文:http://www.cnblogs.com/SinGuLaRiTy2001/p/6622974.html