二叉排序树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉排序树的存储结构。中序遍历二叉排序树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉排序树变成一个有序序列,构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索,插入,删除的复杂度等于树高,O(log(n)).
与堆排序不同。要理解“堆”的概念:一个非常特殊的结构 -- 逻辑上是一颗完全二叉树,但存储上是一个顺序数组(优先队列)
所以,最好不要用链表描述;因为堆在本质上是一个连续的存储空间,只是为了排序,我们把它看成了一颗--完--全--二--叉--树!
一开始node*root=NULL;定义一个空指针,将指向二叉树的根节点。
从已有的数组中读取数值:
先判断当前指针是否为空(递归出口),若为空,则新建一个结构体并:1)将当前数值放入结点。2)使此结点左右指针赋值NULL;
若不是空指针。比较当前数值与结点内num的大小关系。若小于等于num,往左。大于num,往右。(此操作保证左边儿子总小于等于父亲,右儿子总大于父亲,两个相同的数挨着放)
建树完成
从二叉树输出(将树输出至原数组):
以从小到大排序为例(将树输出至原数组):
先判断当前指针是否为空(递归出口),若为空,则return。
因为右边的小,所以向右递归。
右边函数递归结束后输出父亲
最后向左递归。
/*若想从大到小输出则交换第2、4步。*/
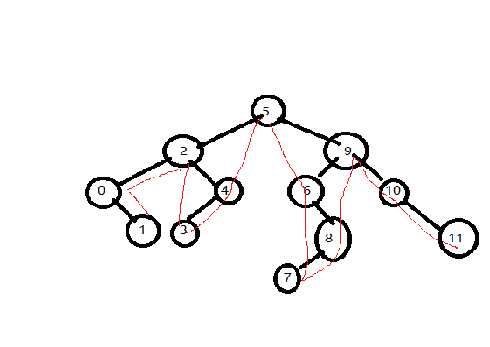
红线为从小到大输出顺序
#include<iostream>
using namespace std;
struct node
{
int num;
node*left;
node*right;
};
void build_tree(node*&p, int x)
{
if (p == NULL)
{
p = new node;
p->left = p->right = NULL;
p->num = x;
return;
}
if (x <= p->num)
{
build_tree(p->left, x);
}
if (x > p->num)
{
build_tree(p->right, x);
}
}
int output(node*&p,int*&ans,int i)
{
if (p == NULL)
return i;
i=output(p->left,ans,i);
ans[i] = p->num; i++;
i=output(p->right,ans,i);
return i;
}
void BST(int*a, int N)
{
node*root = NULL;
int i;
for (i = 0; i < N; i++)
{
build_tree(root, a[i]);
}
output(root,a,0);
}
原文:http://www.cnblogs.com/jinmingyi/p/6648430.html