
题意是把一个二叉树转换成一个链表,链表的元素顺序是二叉树的先序遍历结果。
最简单的做法就是先序遍历该二叉树,将所有经过的节点的指针都依次记录在一个vector里,完成后,在将vector里的节点指针的左孩子置为NULL,右孩子置为vector中的下一个指针。具体的代码和运行效果如下
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 void preOrderTravel(TreeNode* root,vector<TreeNode*>& nodes){ 13 nodes.push_back(root); 14 if(root->left!=NULL) 15 preOrderTravel(root->left,nodes); 16 if(root->right!=NULL) 17 preOrderTravel(root->right,nodes); 18 } 19 void flatten(TreeNode* root) { 20 if(root==NULL)return; 21 vector<TreeNode*> nodes; 22 preOrderTravel(root,nodes); 23 int i=0; 24 for(i=0;i<nodes.size()-1;i++){ 25 nodes[i]->left=NULL; 26 nodes[i]->right=nodes[i+1]; 27 } 28 nodes[i]->left=NULL; 29 nodes[i]->right=NULL; 30 } 31 };
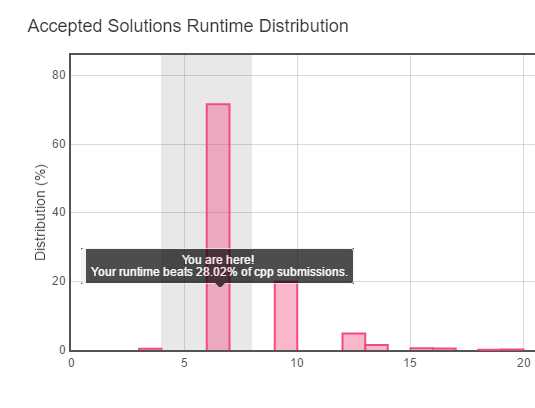
这里用了多余的空间来存储二叉树的节点,是否可以不用多余的空间来实现转换呢?这里就想到了递归思想,既然flatten操作可以完成转换,可不可以先转换根节点的左子树,再转换根节点的右子树,最后再合成完整的二叉树。用例子来推演就可以得到如下的代码,这份代码的空间复杂度是O(1),时间复杂度理论是和上面的代码相同(都是遍历一遍树),但实际从LeetCode运行结果来看,上面的代码更快。具体的代码和运行效果如下:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 TreeNode* prev=NULL; 13 void flatten(TreeNode* root) 14 { 15 if(root==NULL)return; 16 flatten(root->right); 17 flatten(root->left); 18 root->left=NULL; 19 root->right=prev; 20 prev=root; 21 } 22 };
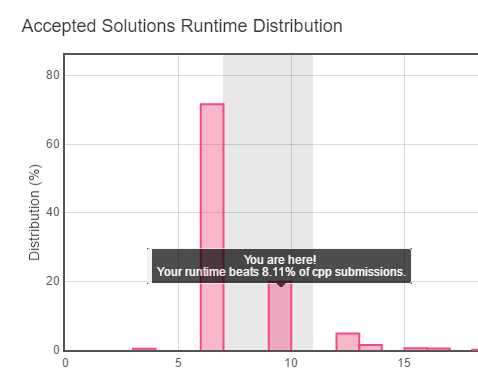
LeetCode 114. Flatten Binary Tree to Linked List
原文:http://www.cnblogs.com/gremount/p/6671222.html