组合数表示的是从n个物品中选出m个物品的方案数。举个例子,从(1,2,3) 三个物品中选择两个物品可以有(1,2),(1,3),(2,3)这三种选择方法。根据组合数的定 义,我们可以给出计算组合数的一般公式:
其中n! = 1 × 2 × · · · × n
小葱想知道如果给定n,m和k,对于所有的0 <= i <= n,0 <= j <= min(i,m)有多少对 (i,j)满足是k的倍数。
输入格式:
第一行有两个整数t,k,其中t代表该测试点总共有多少组测试数据,k的意义见 【问题描述】。
接下来t行每行两个整数n,m,其中n,m的意义见【问题描述】。
输出格式:
t行,每行一个整数代表答案。
1 2 3 3
1
2 5 4 5 6 7
0 7
【样例1说明】
在所有可能的情况中,只有是2的倍数。
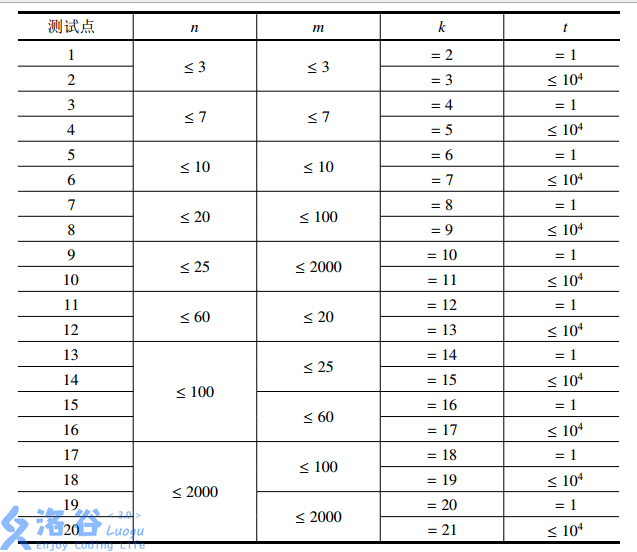
【子任务】
递推+二维前缀和
组合数递推公式:C(i,j)=C(i-1,j)+C(i-1,j-1)
预处理所有组合数%k是否为0,注意递推过程中取模,同时标记%k=0的位置
前缀和统计答案 sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+(模k是否为0)
注意特殊处理0
n²预处理 O(1)查询
#include<cstdio> #include<cstring> using namespace std; int t,k,c[2001][2001],sum[2001][2001],a[2001][2001]; void pre() { for(int i=1;i<=2000;i++) { c[i][0]=1%k,c[i][1]=i%k; if(!c[i][0]) a[i][0]++; if(!c[i][1]) a[i][1]++; } for(int i=2;i<=2000;i++) for(int j=2;j<=i;j++) { c[i][j]=(c[i-1][j]+c[i-1][j-1])%k; if(!c[i][j]) a[i][j]++; } for(int i=1;i<=2000;i++) sum[i][0]=sum[i-1][0]+a[i][0],sum[0][i]=sum[0][i-1]+a[0][i]; for(int i=1;i<=2000;i++) { for(int j=1;j<=2000;j++) sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]; } } int main() { freopen("problem.in","r",stdin); freopen("problem.out","w",stdout); scanf("%d%d",&t,&k); pre(); int n,m; while(t--) { scanf("%d%d",&n,&m); printf("%d\n",sum[n][m]); } return 0; }
两个错误:
1、sum数组没有预处理0,sum[][0-1]出问题了
2、递推过程中第二维j循环到i,不能到2000,对C数组没有影响,
但对a数组来说,c未经赋值为0,错误统计
原文:http://www.cnblogs.com/TheRoadToTheGold/p/6671895.html