【题目】
在n个元素的无序数组中选择第k(1<=k<=n)小元素。
当k=1时,相当于找最小值。
当k=n时,相当于找最大值。
当k=n/2时,称中值。
【要求】
线性时间内完成,即O(n)。
【算法解析】
【核心代码】
template<class Type> Type select (Type a[],int p, int r, int k) { if (r-p<75) { //用某个简单排序算法对数组a[p:r]排序; bubbleSort(a,p,r); return a[p+k-1]; } //将a[p+5*i]至a[p+5*i+4]的第3小元素 //与a[p+i]交换位置; //找中位数的中位数,r-p-4即上面所说的n-5 for ( int i = 0; i<=(r-p-4)/5; i++ ) { int s=p+5*i, t=s+4; for (int j=0;j<3;j++) bubbleSort(a,s,t-j); swap(a, p+i, s+2); } Type x = select(a,p, p+(r-p-4)/5, (r-p+6)/10); int i=partition(a,p,r,x),j=i-p+1; if (k<=j) return select(a,p,i,k); else return select(a,i+1,r,k-j); }
【完整代码】
#include <iostream> using namespace std; template<class Type> void swap(Type a[],int p,int r){ Type temp=a[p]; a[p]=a[r]; a[r]=temp; } template<class Type> void bubbleSort(Type a[],int p,int r){ int lastSwapPos = 0,lastSwapPosTemp = 0; for (int i = p; i < r; i++) { lastSwapPos = lastSwapPosTemp; for (int j = r; j >lastSwapPos; j--) { if (a[j - 1] > a[j]){ swap(a,j-1,j); lastSwapPosTemp = j; } } if (lastSwapPos == lastSwapPosTemp) break; } } template <class T> int partition (T a[], const int p, const int r,T x) { int pivotpos = p; for (int i = p; i <= r; i++) if (a[i] < x) { pivotpos++; if (pivotpos != i){ swap(a,pivotpos,i); } } return pivotpos; } template<class Type> Type select (Type a[],int p, int r, int k){ if (r-p<75) { //对数组a[p:r]排序; bubbleSort(a,p,r); return a[p+k-1]; } //将a[p+5*i]至a[p+5*i+4]的第3小元素 //与a[p+i]交换位置; //找中位数的中位数,r-p-4即上面所说的n-5 for ( int i = 0; i<=(r-p-4)/5; i++ ){ int s=p+5*i, t=s+4; for (int j=0;j<3;j++) bubbleSort(a,s,t-j); swap(a, p+i, s+2); } Type x = select(a,p, p+(r-p-4)/5, (r-p+6)/10); int i=partition(a,p,r,x),j=i-p+1; if (k<=j) return select(a,p,i,k); else return select(a,i+1,r,k-j); } int main() { //int a[]={0,6,5,1}; //int a[]={1,2,3,4,5,6,7,8,9,10}; int a[]={1,29,3,4,5,9,7,855,97,100}; cout<<select(a,0,9,10); return 0; }
【时间复杂度】
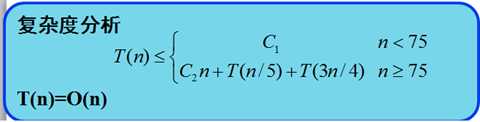
原文:http://www.cnblogs.com/wxgblog/p/xianxingshijianxuanzhe.html