【问题】
有一个贼在偷窃一家商店时发现有N件物品;第i件物品值pi元,重wi磅(1≤i≤N),且都是整数。
他希望带走的东西越值钱越好,但他的背包中最多能装下M磅的东西(整数)。
如果每件物品或被带走或被留下,小偷应该带走哪几样东西?
【算法解析】
令f(i,y) 表示容量为y,物品i,i+1,···,n 的优化效益值,按优化原理可列递归关系如下:
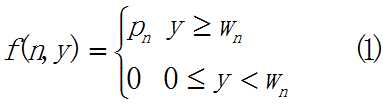
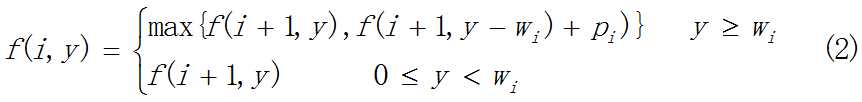
初始背包问题的递归方程
f(1,c)=max{f(2,c), f(2,c-w1)+p1}
迭代
计算从f(n, *)开始((1)式)
然后应用(2)式递归计算f(i,*) ( i=n-1,n-2,···,2 ),
最后得出 f(1,c)
【代码】
(1)递归解法:
#include <iostream> using namespace std; const int n=3; int w[n]={100,14,10}; int p[n]={20,18,15}; int F(int i, int y) { if (i == n) return (y < w[n]) ? 0 : p[n]; if (y < w[i]) return F(i+1,y); return max(F(i+1,y), F(i+1,y-w[i]) + p[i]); } int main() { cout<<F(0,116); return 0; }
原文:http://www.cnblogs.com/wxgblog/p/0-1beibaowenti.html