第一节:旋转
1.2D中的旋转
上一节中讲了矩阵的几何意义,矩阵的每一行可以看做该维度向量的分解坐标轴向量所对应的最终状态。接下来我们以2D单位向量来讨论2D向量的旋转问题。
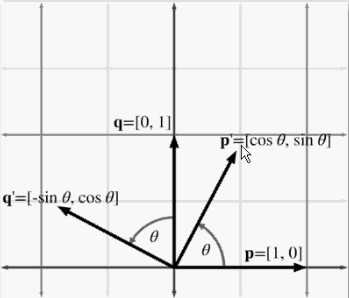
上图中我们以2D向量[1 1]来演示旋转θ角后的矩阵表示。首先分解2D向量[1 1],然后[1 1]向量的旋转其实就是分解的p和q向量的旋转,旋转后得到的p‘和q‘向量就是旋转后的向量。我们可以根据三角函数求出旋转后的分解向量p‘和q‘。然后我们根据矩阵的几何定义,可以推理出2D向量的旋转矩阵。
原文:http://www.cnblogs.com/metalsteel/p/6687008.html