[Sdoi2017]数字表格-布布扣-bubuko.com

[Sdoi2017]数字表格

http://www.lydsy.com/JudgeOnline/problem.php?id=4816

Time Limit: 50 Sec Memory Limit: 128 MB

Description

Doris刚刚学习了fibonacci数列。用f[i]表示数列的第i项，那么

f[0]=0

f[1]=1

f[n]=f[n-1]+f[n-2],n>=2

Doris用老师的超级计算机生成了一个n×m的表格，第i行第j列的格子中的数是f[gcd(i,j)]，其中gcd(i,j)表示i,

j的最大公约数。Doris的表格中共有n×m个数，她想知道这些数的乘积是多少。答案对10^9+7取模。

Input

有多组测试数据。

第一个一个数T，表示数据组数。

接下来T行，每行两个数n,m

T<=1000,1<=n,m<=10^6

Output

输出T行，第i行的数是第i组数据的结果

Sample Input

3
2 3
4 5
6 7

Sample Output

1
6
960

g（d）转化为 POI 2007 Zap

题目即解释参考 http://www.cnblogs.com/TheRoadToTheGold/p/6609495.html

转化提示：1、a^b * c^b = (a*c)^d

2、a^(b*c) = (a^b)^c

预处理g的时候会遇到 mul=-1，所以要处理逆元

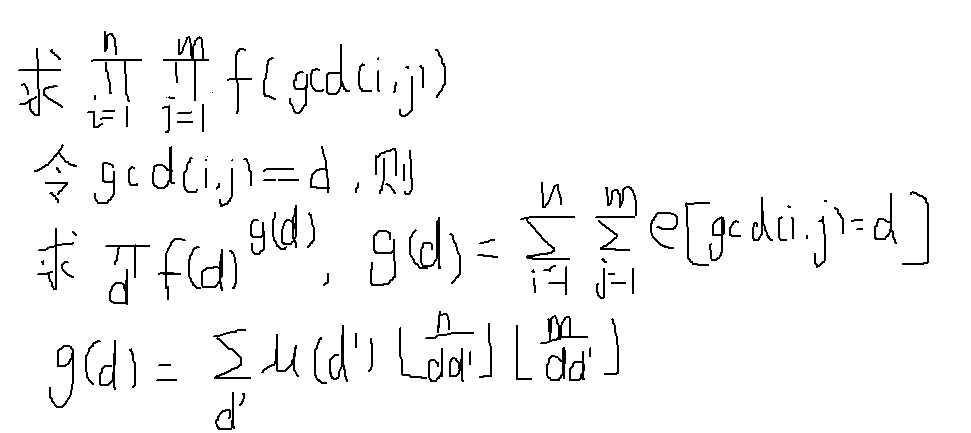
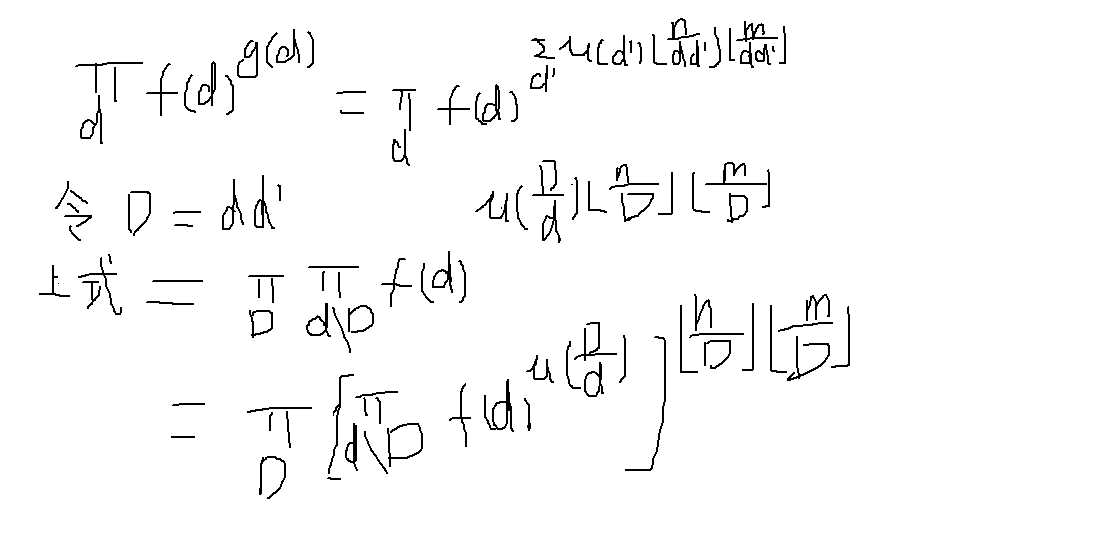
#include<cstdio>
#include<iostream>
#define N 1000101
using namespace std;
int mul[N],prime[N],cnt;
long long f[N],g[N],inver[N];
const int mod=1e9+7;
bool v[N];
int n,m;
long long mult(long long a,long long b )
{
    long long ans=1;
    for(;b;b>>=1,a=a*a%mod)
     if(b&1) ans=ans*a%mod;
    return ans;
}
void pre()
{
    mul[1]=1;
    for(int i=2;i<N;i++)
    {
        if(!v[i])
        {
            prime[++cnt]=i;
            mul[i]=-1;
        }
        for(int j=1;j<=cnt;j++)
        {
            if(prime[j]*i>N-1) break;
            v[i*prime[j]]=true;
            if(i%prime[j]==0) break;
            mul[i*prime[j]]=-mul[i];
        }
    }
    f[1]=1;
    for(int i=2;i<N;i++) f[i]=(f[i-1]+f[i-2])%mod;
    for(int i=1;i<N;i++) inver[i]=mult(f[i],mod-2);
    fill(g,g+N,1);
    for(int i=1;i<N;i++)
     for(int j=1;i*j<N;j++)
      if(mul[j])  g[i*j]= g[i*j]*(mul[j]==1 ? f[i] : inver[i])%mod;
    for(int i=1;i<N;i++) g[i]=g[i-1]*g[i]%mod;
}
void solve()
{
    long long ans=1;int j;
    if(n>m) swap(n,m);
    for(int i=1;i<=n;i=j+1)
    {
        j=min(n/(n/i),m/(m/i));
        ans=ans*mult(g[j]*mult(g[i-1],mod-2)%mod,(long long)(n/i)*(m/i))%mod;
    }
    printf("%lld\n",ans);
}
int main()
{
    /*freopen("product.in","r",stdin);
    freopen("product.out","w",stdout);*/
	pre();
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        solve();
    }
}

[Sdoi2017]数字表格

原文：http://www.cnblogs.com/TheRoadToTheGold/p/6702237.html