自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?
自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?
第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1
一个整数,表示不同的满足要求的树的个数,无解输出0
两棵树分别为1-2-3;1-3-2
prufer编码相关。
1.找到编号最小的叶节点,删除这个节点,然后与这个叶节点相连的点计入序列
2.反复进行1,直到这棵树只剩下两个节点时,退出
这是prufer编码的过程 一个prufer编码对应一棵树,反之一棵树对应一个prufer编码。
那么一个节点会在prufer编码中出现的几次呢?应该是他的度数-1 当度数不为1时 总会删掉他的一个叶子节点 就在prufer编码中出现一次,当他变成叶子结点时,那么他就不会在prufer编码中出现,这时他的度数为1。
这道题有些度数是不确定的,我们先考虑确定的部分:
确定的部分的每个点在prufer编码中出现的次数为d-1 prufer编码长n-2 也就是说在编码中放的方案数是C(d1-1,n-2)
然后n-2中有d1-1个位置被占掉了,那么下一个就有n-2-d1+1个位置可以放,方案数是C(d2-1,n-d1-1) 以此类推,确定度数的方案数求好了。
那么剩下的不确定的呢?因为之前确定的点已经放好了,那么他们不会出现在后面的编码中,那么设剩下的点的数量为m,位置还有n-2-sigma(di-1),因为每个位置可以随意放任意一个没有确定的数,这样做是符合prufer编码的,那么每个位置有m个可能,位置有n-2-sigma(di-1),那么没确定的方案数就是m^(n-2-sigma(di-1))。
这里还要用高精度 这个式子还可以化简成这个样子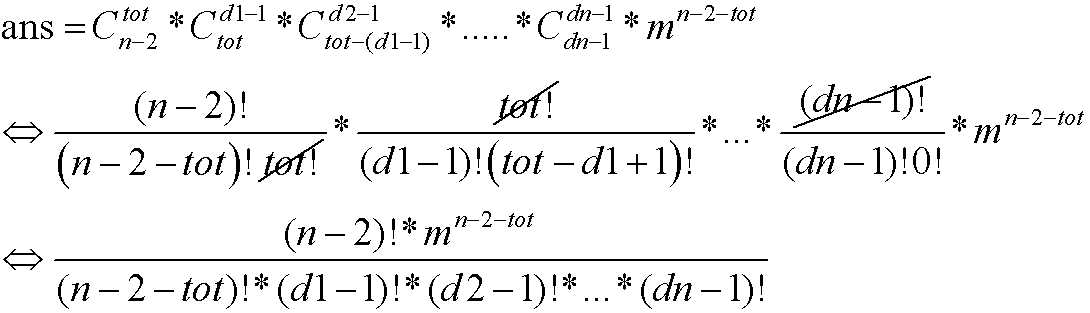
高精度很好写,因为每次是低精度*高精度,然后我又学到了压位的技巧。

#include<bits/stdc++.h> using namespace std; const int N = 10010, M = 10000; int n, sum, len, degree; int pri[N], b[N], table[N]; namespace BIG { int num[N]; void mul(int x) { for(int i = 1; i <= len; ++i) num[i] *= x; for(int i = 1; i <= len; ++i) { num[i + 1] += num[i] / M; num[i] %= M; } while(num[len + 1] >= M) { num[len + 2] += num[len + 1] / M; num[len + 1] %= M; ++len; } if(num[len + 1]) ++len; } void print() { for(int i = len; i; --i) if(i == len) printf("%d", num[i]); else printf("%04d", num[i]); } } using namespace BIG; bool isprime(int x) { for(int i = 2; i * i <= x; ++i) if(x % i == 0) return false; return true; } void Init() { for(int i = 2; i <= 1000; ++i) if(isprime(i)) pri[++pri[0]] = i; } void solve(int x, int f) { for(int i = 1; i <= pri[0]; ++i) while(x % pri[i] == 0 && x) { table[pri[i]] += f; x /= pri[i]; } } int main() { // freopen("bzoj_1005.in", "r", stdin); // freopen("bzoj_1005.out", "w", stdout); Init(); scanf("%d", &n); if(n == 1) { int x; scanf("%d", &x); if(x == 1) puts("0"); else puts("1"); return 0; } for(int i = 1; i <= n; ++i) { int x; scanf("%d", &x); if(!x) { puts("0"); return 0; } if(x != -1) b[++b[0]] = x - 1, sum += x - 1; degree += x == -1 ? n : x - 1; } if(sum > n - 2 || degree < n - 1) { puts("0"); return 0; } num[++len] = 1; solve(n - b[0], n - 2 - sum); for(int i = n - 1 - sum; i <= n - 2; ++i) solve(i, 1); for(int i = 1; i <= b[0]; ++i) for(int j = 2; j <= b[i]; ++j) solve(j, -1); for(int i = 1; i <= pri[0]; ++i) if(table[pri[i]]) for(int j = 1; j <= table[pri[i]]; ++j) mul(pri[i]); print(); // fclose(stdin); fclose(stdout); return 0; }
原文:http://www.cnblogs.com/19992147orz/p/6715882.html