最近点对问题的解法

回到二维的情况。参考一维退化版本的解法，首先进行分解和求解步骤。

1. 分解：将所有点按照横坐标从中心分成两部分。

2. 求解：递归求解两半部分的最近点对，左右两半部分依次为 p_1,p_2p?1??,p?2?? 和 q_1,q_2q?1??,q?2??。

3. 合并：令 d = min\{|p_1-p_2|, |q_1-q_2|\}d=min{∣p?1??−p?2??∣,∣q?1??−q?2??∣}。如下左图所示，除了两半部分各自的最近点对之外，只需要计算横跨图中左右两半部分区域的点对的距离最小值，再和 dd 进行比较即可。

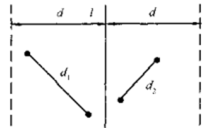
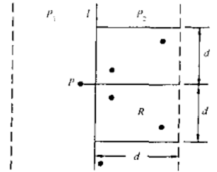
首先极端情况下，会有总共 nn 个点落在左图中这宽为 2d2d 的区域中。然而我们考虑固定其中一边的某个点 PP，和其对应的另一个点一定会落在右图中右半部分的 d \times 2dd×2d 的区域中。根据鸽巢原理，在另一边中最多只需要检查 66 个点。

具体的证明就不在这里展开讲了，我们重点还是学习这个算法中的分治思想。

最终合并的过程为：

1. 首先将在左图中宽为 2d2d 区间内的点按纵坐标排序；
2. 之后顺序枚举所有落在这个 2d2d 区域中的点，并计算与其纵坐标差不超过 dd 的点的距离。

最近点对问题的解法

原文：http://www.cnblogs.com/upstart/p/6764957.html