一、开运算
开运算,就是先腐蚀后膨胀的过程
数学表达式:
dst = open(src,element) = dilate(erode(src, element))
开运算可以用来消除小物体,在纤细点处分离物体,并且在平滑较大物体的边界的同时不明显改变其面积。
二、闭运算
闭运算,就是先膨胀后腐蚀的过程
数学表达式:
dst = open(src,element) = erode(dilate(src, element))
闭运算可以用来排除小型黑洞(黑色区域)
三、形态学梯度
形态学梯度,就是膨胀图与腐蚀图之差
数学表达式:
dst = morph-grad(src,element) = dilate(src, element) - erode(src, element)
对二值图进行这一操作可以将团块的边缘突出出来,我们可以用形态学梯度来保留物体的边缘轮廓
四、顶帽
顶帽(礼帽)运算,就是原图像与“开运算”的结果图之差
数学表达式:
dst = tophat(src,element) = src - open(src,element)
因为开运算带来的结果是放大了裂缝或者局部低亮度的区域。因此从原图中减去开运算后的图,得到的效果
图突出了比原图轮廓周围的区域更明亮的区域,且这一操作与选择的核的的大小相关。
顶帽运算往往用来分离比临近点亮一些的斑块,在一幅图像具有大幅的背景,而微小物品比较有规律的情况下,
可以使用顶帽运算进行背景提取
五、黑帽
黑帽运算,就是“闭运算”的结果图与原图像之差
数学表达式:
dst = blackhat(src,element) = close(src,element) - src
黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域,且这一操作和选择的核的大小相关
黑帽运算用来分离比临近点暗一些的斑块,效果图有着非常完美的轮廓


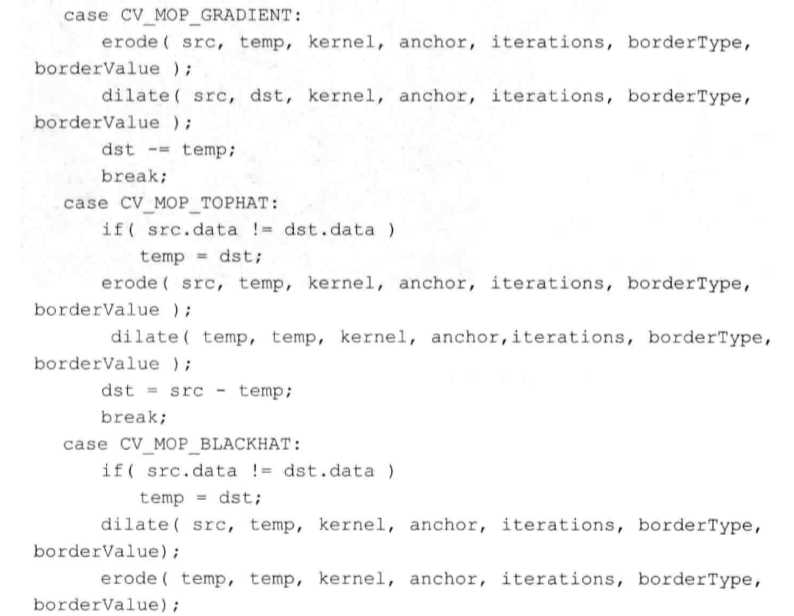

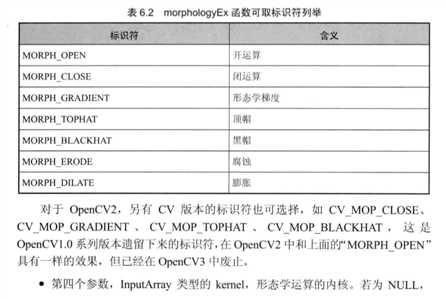
六、核心函数:morphologyEx()
1 void morphologyEx( InputArray src, OutputArray dst, 2 int op, InputArray kernel, 3 Point anchor = Point(-1,-1), int iterations = 1, 4 int borderType = BORDER_CONSTANT, 5 const Scalar& borderValue = morphologyDefaultBorderValue() );



原文:http://www.cnblogs.com/Nelsoner/p/6783477.html