https://vjudge.net/problem/UVA-11768
题意:
给定两个点A(x1,y1)和B(x2,y2),均为0.1的整数倍。统计选段AB穿过多少个整点。
思路:
做了这道题之后对于扩展欧几里得有了全面的了解。
根据两点式公式求出直线 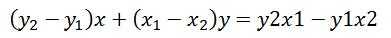 ,那么ax+by=c 中的a、b、c都可以确定下来了。
,那么ax+by=c 中的a、b、c都可以确定下来了。
接下来首先去计算出一组解(x0,y0),因为根据这一组解,你可以写出它的任意解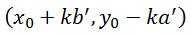 ,其中
,其中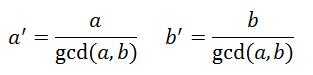 ,K取任何整数。
,K取任何整数。
需要注意的是,这个 a‘ 和 b‘ 是很重要的,比如说 b‘ ,它代表的是x每隔 b‘ ,就会出现一个整点。
所以这道题目的关键就是,我们先求出一组解,然后通过它的 b‘ 将x0改变成x,使得x在[x1,x2]区间之内,这样每 b‘ 个单位就有一个整点了,即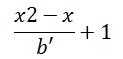
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<vector> 6 #include<stack> 7 #include<queue> 8 #include<cmath> 9 #include<map> 10 using namespace std; 11 12 typedef long long LL; 13 double X1,Y1,X2,Y2; 14 15 void gcd(LL a,LL b,LL& d,LL& x,LL& y) 16 { 17 if(!b) {d=a;x=1;y=0;} 18 else { gcd(b,a%b,d,y,x); y-=x*(a/b);} 19 } 20 21 LL solve() 22 { 23 LL x1=X1*10, y1=Y1*10, x2=X2*10, y2=Y2*10; 24 if(x1==x2) //平行y轴 25 { 26 if(x1%10) return 0; //原来的X1为小数,肯定不是整点 27 if(Y2<Y1) swap(Y1,Y2); 28 return floor(Y2)-ceil(Y1)+1; 29 } 30 if(y1==y2) 31 { 32 if(y1%10) return 0; 33 if(X2<X1) swap(X1,X2); 34 return floor(X2)-ceil(X1)+1; 35 } 36 LL a=(y2-y1)*10, b=(x1-x2)*10, c=y2*x1-y1*x2; //c相当于扩大了100倍,所以前面还得乘10 37 LL d,x,y; 38 gcd(a,b,d,x,y); 39 if(c%d) return 0; //扩展欧几里得算法无解的判断 40 41 x=x*c/d; y=y*c/d; //获得一组整数解(x,y) 42 b=abs(b/d); //这里的b其实就是b‘ 43 44 if(X1>X2) swap(X1,X2); 45 x1=ceil(X1); 46 x2=floor(X2); 47 if(x1>x2) return 0; 48 49 x=x+(x1-x)/b*b; //使x进入[x1,x2]的区间内 50 if(x<x1) x+=b; 51 if(x>x2) return 0; 52 return (x2-x)/b+1; 53 } 54 55 int main() 56 { 57 //freopen("D:\\input.txt","r",stdin); 58 int T; 59 scanf("%d",&T); 60 while(T--) 61 { 62 scanf("%lf%lf%lf%lf",&X1,&Y1,&X2,&Y2); 63 LL ans = solve(); 64 printf("%lld\n",ans); 65 } 66 return 0; 67 }
原文:http://www.cnblogs.com/zyb993963526/p/6783532.html