MasterMind is a game for two players. One of them, Designer, selects a secret code. The other, Breaker, tries to break it. A code is no more than a row of colored dots. At the beginning of a game, the players agree upon the length N that a code must have and upon the colors that may occur in a code.
In order to break the code, Breaker makes a number of guesses, each guess itself being a code. After each guess Designer gives a hint, stating to what extent the guess matches his secret code.
In this problem you will be given a secret code and a guess , and are to determine the hint. A hint consists of a pair of numbers determined as follows.
A match is a pair (i,j), and , such that . Match (i,j) is called strong when i =j, and is called weak otherwise. Two matches (i,j) and (p,q) are called independent when i = p if and only if j = q. A set of matches is called independent when all of its members are pairwise independent.
Designer chooses an independent set M of matches for which the total number of matches and the number of strong matches are both maximal. The hint then consists of the number of strong followed by the number of weak matches in M. Note that these numbers are uniquely determined by the secret code and the guess. If the hint turns out to be (n,0), then the guess is identical to the secret code.
The input will consist of data for a number of games. The input for each game begins with an integer specifying N (the length of the code). Following these will be the secret code, represented as N integers, which we will limit to the range 1 to 9. There will then follow an arbitrary number of guesses, each also represented as N integers, each in the range 1 to 9. Following the last guess in each game will be N zeroes; these zeroes are not to be considered as a guess.
Following the data for the first game will appear data for the second game (if any) beginning with a new value for N. The last game in the input will be followed by a single zero (when a value for N would normally be specified). The maximum value for N will be 1000.
The output for each game should list the hints that would be generated for each guess, in order, one hint per line. Each hint should be represented as a pair of integers enclosed in parentheses and separated by a comma. The entire list of hints for each game should be prefixed by a heading indicating the game number; games are numbered sequentially starting with 1. Look at the samples below for the exact format.
4 1 3 5 5 1 1 2 3 4 3 3 5 6 5 5 1 6 1 3 5 1 3 5 5 0 0 0 0 10 1 2 2 2 4 5 6 6 6 9 1 2 3 4 5 6 7 8 9 1 1 1 2 2 3 3 4 4 5 5 1 2 1 3 1 5 1 6 1 9 1 2 2 5 5 5 6 6 6 7 0 0 0 0 0
Game 1:
(1,1)
(2,0)
(1,2)
(1,2)
(4,0)
Game 2:
(2,4)
(3,2)
(5,0)
(7,0)
这道题不能不让我想起新生赛那到题,两道题意思相差不是很多,都是猜数字,统计有多少数字位置正确(f1),有多少数字在两个序列都出现过但位置不对(f2),
一行数字全为0结束,所以我的思路就是分别写两个循环,找到f1,f2。因为出现的数字会相同,我怕我没有统计多次,所以用vis,vi来标记了出现的数字。

#include<bits/stdc++.h> using namespace std; const int N=1005; int a[N],q[N],vi[N],vis[N]; int main() { int k=0,n; while (scanf("%d",&n)!=EOF,n){ printf("Game %d:\n",++k); for (int i=1;i<=n;i++) scanf("%d",&a[i]); for(;;){ for (int i=1;i<=n;i++) scanf("%d",&q[i]); int s=0; for (int i=1;i<=n;i++) s+=q[i]; if(s){ int f1=0,f2=0; memset(vi,0,sizeof(vi)); memset(vis,0,sizeof(vis)); for (int i=1;i<=n;i++) if (a[i]==q[i]){ vi[i]=1; vis[i]=1; f1++; } for (int i=1;i<=n;i++){ for (int j=1;j<=n;j++){ if (a[i]==q[j]&&!vi[i]&&!vis[j]){ f2++; vi[i]=1; vis[j]=1; } } } printf(" (%d,%d)\n",f1,f2);} else break; } } return 0; }
For a positive integer N , the digit-sum of N is defined as the sum of N itself and its digits. When M is the digitsum ofN , we call N a generator of M .
For example, the digit-sum of 245 is 256 (= 245 + 2 + 4 + 5). Therefore, 245 is a generator of 256.
Not surprisingly, some numbers do not have any generators and some numbers have more than one generator. For example, the generators of 216 are 198 and 207.
You are to write a program to find the smallest generator of the given integer.
Your program is to read from standard input. The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case takes one line containing an integer N , 1N100, 000 .
Your program is to write to standard output. Print exactly one line for each test case. The line is to contain a generator of N for each test case. If N has multiple generators, print the smallest. If N does not have any generators, print 0.
The following shows sample input and output for three test cases.
3 216 121 2005
198 0 1979
这道题题意也很简单啦,就是找一个比n小的数,这个数和它的每一位相加的和等于n,不就是暴力穷举么,不过从哪一位开始需要考虑下,一个数字最大9,它的每一位都是9
的话,也就是9*n的位数,这个就是你穷举的开始,然后直接暴力一下就好的。

#include<stdio.h> int main() { int t; scanf ("%d", &t); while (t--) { int n; scanf ("%d", &n); int ans = 0; int a=n,w=0; while(a){ w++; a/=10; } for (int i = n-w*9; i < n; i++) { int a =i, b = i; while (b) { a += b % 10; b /= 10; } if (a == n) { ans = i; break; } } printf ("%d\n", ans); } return 0; }
Some DNA sequences exist in circular forms as in the following figure, which shows a circular sequence ``CGAGTCAGCT", that is, the last symbol ``T" in ``CGAGTCAGCT" is connected to the first symbol ``C". We always read a circular sequence in the clockwise direction.
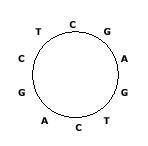
Since it is not easy to store a circular sequence in a computer as it is, we decided to store it as a linear sequence. However, there can be many linear sequences that are obtained from a circular sequence by cutting any place of the circular sequence. Hence, we also decided to store the linear sequence that is lexicographically smallest among all linear sequences that can be obtained from a circular sequence.
Your task is to find the lexicographically smallest sequence from a given circular sequence. For the example in the figure, the lexicographically smallest sequence is ``AGCTCGAGTC". If there are two or more linear sequences that are lexicographically smallest, you are to find any one of them (in fact, they are the same).
The input consists of T test cases. The number of test cases T is given on the first line of the input file. Each test case takes one line containing a circular sequence that is written as an arbitrary linear sequence. Since the circular sequences are DNA sequences, only four symbols, A, C, G and T, are allowed. Each sequence has length at least 2 and at most 100.
Print exactly one line for each test case. The line is to contain the lexicographically smallest sequence for the test case.
The following shows sample input and output for two test cases.
2 CGAGTCAGCT CTCC
AGCTCGAGTC CCCT
又是AGCT,又是DNA,这不是运载体什么的环状DNA么,看样例读题意就是找到从环上那个点开始使它的字典序最小,这不是直接套string么,很短很易懂。

#include<bits/stdc++.h> using namespace std; int main(){ int t; cin>>t; while(t--){ string s; cin>>s; string mi=s; for(int i=1;s[i];i++){ string c=s.substr(i)+s.substr(0,i); if(mi>c) mi=c; } cout<<mi<<endl; } }
There is an objective test result such as ``OOXXOXXOOO". An `O‘ means a correct answer of a problem and an `X‘ means a wrong answer. The score of each problem of this test is calculated by itself and its just previous consecutive `O‘s only when the answer is correct. For example, the score of the 10th problem is 3 that is obtained by itself and its two previous consecutive `O‘s.
Therefore, the score of ``OOXXOXXOOO" is 10 which is calculated by ``1+2+0+0+1+0+0+1+2+3".
You are to write a program calculating the scores of test results.
Your program is to read from standard input. The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case starts with a line containing a string composed by `O‘ and `X‘ and the length of the string is more than 0 and less than 80. There is no spaces between `O‘ and `X‘.
Your program is to write to standard output. Print exactly one line for each test case. The line is to contain the score of the test case.
The following shows sample input and output for five test cases.
5 OOXXOXXOOO OOXXOOXXOO OXOXOXOXOXOXOX OOOOOOOOOO OOOOXOOOOXOOOOX
10 9 7 55 30
这个就更简单了,题都没怎么看直接看的样例,看到了这句话"the score of ``OOXXOXXOOO" is 10 which is calculated by ``1+2+0+0+1+0+0+1+2+3".",
心里就更踏实了,对一个加一分,连对几个加几分。

#include<stdio.h> int main() { int t; scanf ("%d", &t); getchar(); while (t--) { char s[105]; gets(s); int a=0,sum=0; for(int i=0;s[i];i++){ if(s[i]==‘O‘){ a++; sum+=a;} else a=0; } printf("%d\n",sum); } return 0; }
Ivan works at a factory that produces heavy machinery. He has a simple job — he knocks up wooden
boxes of different sizes to pack machinery for delivery to the customers. Each box is a rectangular
parallelepiped. Ivan uses six rectangular wooden pallets to make a box. Each pallet is used for one side
of the box.
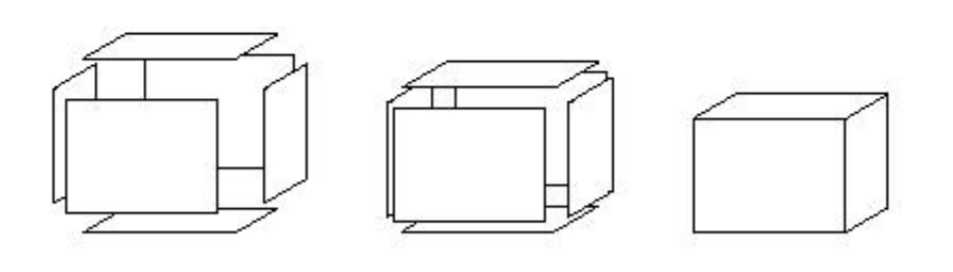
Joe delivers pallets for Ivan. Joe is not very smart and often makes mistakes — he brings Ivan
pallets that do not fit together to make a box. But Joe does not trust Ivan. It always takes a lot of
time to explain Joe that he has made a mistake.
Fortunately, Joe adores everything related to computers and sincerely believes that computers never
make mistakes. Ivan has decided to use this for his own advantage. Ivan asks you to write a program
that given sizes of six rectangular pallets tells whether it is possible to make a box out of them.
Input
Input file contains several test cases. Each of them consists of six lines. Each line describes one pallet
and contains two integer numbers w and h (1 ≤ w, h ≤ 10 000) — width and height of the pallet in
millimeters respectively.
Output
For each test case, print one output line. Write a single word ‘POSSIBLE’ to the output file if it is
possible to make a box using six given pallets for its sides. Write a single word ‘IMPOSSIBLE’ if it is not
possible to do so.
Sample Input
1345 2584
2584 683
2584 1345
683 1345
683 1345
2584 683
1234 4567
1234 4567
4567 4321
4322 4567
4321 1234
4321 1234
Sample Output
POSSIBLE
IMPOSSIBLE
这道题就是检验啊,检验给你的6个面是不是长方体,这6个面你要单独保存会比较好?我是没有,但是我感觉那样思路应该更清晰,其实也就是两两配对,拿flag标记下,
然后就wa了,想了想长方体三边是a,b,c那么每两组之间必有两个数会想等的,加上这个条件就AC了。

#include <bits/stdc++.h> using namespace std; int main() {int a[12]; while(cin>>a[0]>>a[1]>>a[2]>>a[3]>>a[4]>>a[5]>>a[6]>>a[7]>>a[8]>>a[9]>>a[10]>>a[11]){ sort(a,a+2); sort(a+2,a+4); sort(a+4,a+6); sort(a+6,a+8); sort(a+8,a+10); sort(a+10,a+12); int f[6]; for(int i=0;i<6;i++) f[i]=1; int s=1; for(int i=0;i<12;i+=2){ if(f[i/2]) for(int j=i+2;j<12;j+=2) if(f[j/2]){ if(a[i]==a[j]&&a[i+1]==a[j+1]) f[i/2]=f[j/2]=0; else if(!(a[i]==a[j]||a[i+1]==a[j+1]||a[i]==a[j+1]||a[i+1]==a[j])) s=0; } } for(int i=0;i<6;i++) if(f[i]) {s=0;break;} if(s)printf("POSSIBLE\n"); else printf("IMPOSSIBLE\n"); } return 0;}
A research laboratory of a world-leading automobile company has received an order to create a special transmission mechanism, which allows for incredibly efficient kickdown -- an operation of switching to lower gear. After several months of research engineers found that the most efficient solution requires special gears with teeth and cavities placed non-uniformly. They calculated the optimal flanks of the gears. Now they want to perform some experiments to prove their findings.
The first phase of the experiment is done with planar toothed sections, not round-shaped gears. A section of length n consists of n units. The unit is either a cavity of height h or a tooth of height 2h . Two sections are required for the experiment: one to emulate master gear (with teeth at the bottom) and one for the driven gear (with teeth at the top).
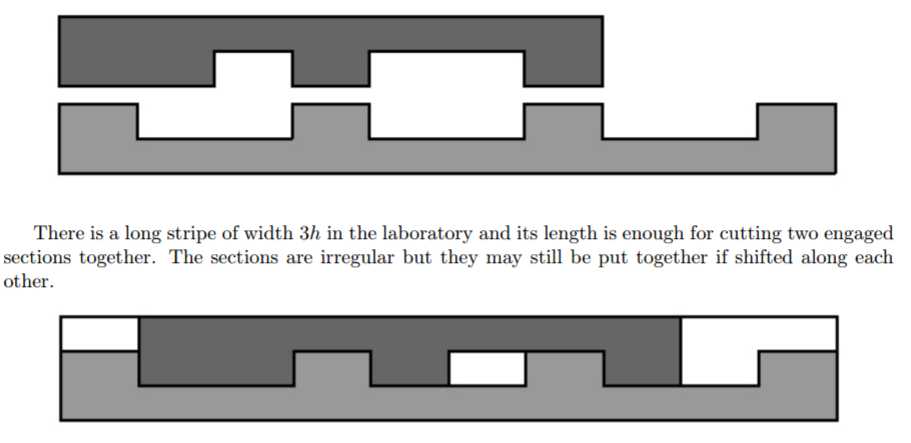
There is a long stripe of width 3h in the laboratory and its length is enough for cutting two engaged sections together. The sections are irregular but they may still be put together if shifted along each other.
The stripe is made of an expensive alloy, so the engineers want to use as little of it as possible. You need to find the minimal length of the stripe which is enough for cutting both sections simultaneously.
The input file contains several test cases, each of them as described below.
There are two lines in the input, each contains a string to describe a section. The first line describes master section (teeth at the bottom) and the second line describes driven section (teeth at the top). Each character in a string represents one section unit -- 1 for a cavity and 2 for a tooth. The sections can not be flipped or rotated.
Each string is non-empty and its length does not exceed 100.
For each test case, write to the output a line containing a single integer number -- the minimal length of the stripe required to cut off given sections.
2112112112
2212112
12121212
21212121
2211221122
21212
10
8
15
这种不就很像牙齿咬合,上下两个值不能超过3,拿字符串模拟啊,但是好像结束条件要考虑清楚,而且这是线段相交的感觉,既可能在左端,也可以在右端,两边都需要考虑
但其实也不就是复制改下两个字符串不就好了。但是中间会有些奇怪的问题,比如你匹配后剩下的长度,当然是选择最长的啦,这个当时迷了,调了好一会。

#include<bits/stdc++.h> using namespace std; int main(){ string s,c; while(cin>>s>>c) {int mi=s.length()+c.length(); for(int i=0;s[i];i++){ int f=1; for(int j=0;c[j];j++){ if(s[i+j]==0)break; if(s[i+j]+c[j]>3+2*‘0‘){ f=0; break; }} if(f){ int t=i+max(c.length(),s.length()-i); if(t<mi) mi=t; } } for(int i=0;c[i];i++){ int f=1; for(int j=0;s[j];j++){ if(c[i+j]==0)break; if(c[i+j]+s[j]>3+2*‘0‘){ f=0; break; }} if(f){ int t=i+max(c.length()-i,s.length()); if(t<mi) mi=t; } } cout<<mi<<endl;} return 0; }
Floating-point numbers are represented differently in computers than integers. That is why a 32-bitfloating-point number can represent values in the magnitude of 10^38 while a 32-bit integer can onlyrepresent values as high as 2^32.
Although there are variations in the ways floating-point numbers are stored in Computers, in thisproblem we will assume that floating-point numbers are stored in the following way:
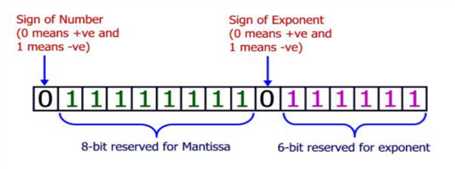
Floating-point numbers have two parts mantissa and exponent. M-bits are allotted for mantissaand E bits are allotted for exponent. There is also one bit that denotes the sign of number (If thisbit is 0 then the number is positive and if it is 1 then the number is negative) and another bit thatdenotes the sign of exponent (If this bit is 0 then exponent is positive otherwise negative). The value ofmantissa and exponent together make the value of the floating-point number. If the value of mantissais m then it maintains the constraints 12 ≤ m < 1. The left most digit of mantissa must always be 1 tomaintain the constraint 12 ≤ m < 1. So this bit is not stored as it is always 1. So the bits in mantissaactually denote the digits at the right side of decimal point of a binary number (Excluding the digitjust to the right of decimal point)
In the figure above we can see a floating-point number where M = 8 and E = 6. The largest valuethis floating-point number can represent is (in binary)
0.111111111(2)×2^111111(2). The decimal equivalentto this number is: 0.998046875 × 2^63 = 9205357638345293824(10). Given the maximum possible valuerepresented by a certain floating point type, you will have to find how many bits are allotted formantissa (M) and how many bits are allotted for exponent (E) in that certain type.
The input file contains around 300 line of input. Each line contains a floating-point number F thatdenotes the maximum value that can be represented by a certain floating-point type. The floating pointnumber is expressed in decimal exponent format. So a number AeB actually denotes the value A×10^B.A line containing ‘0e0’ terminates input. The value of A will satisfy the constraint 0 < A < 10 andwill have exactly 15 digits after the decimal point.
For each line of input produce one line of output. This line contains the value of M and E. You canassume that each of the inputs (except the last one) has a possible and unique solution. You can alsoassume that inputs will be such that the value of M and E will follow the constraints: 9 ≥ M ≥ 0 and30 ≥ E ≥ 1. Also there is no need to assume that (M + E + 2) will be a multiple of 8.
这道题很熟悉,它用科学计数法表示了一个数,你需要计算它的尾数和它的阶码所需的最小位数,这个题是自己找到别人的题解才做出来的。我当时处理e用string转换出了点
问题,说什么这个头文件里不包括这个函数,只好就有c语言的sscannf了,一查其实是c++标准的问题
300行还是不小的,需要先用打表把需要的数据
都预理下,然后比较找到i,j就直接输出。
下面这个是那个老哥的推理,不懂预处理的可以看下,理解这个是这道题的关键,但是其实也就是数学,要用log10处理下,想不明白的可以私聊我
因为位数自带一个1,这个1是不被存储的,所以对于某个i位二进制数的尾数,它的十进制尾数值m=1-2^(-i-1)对于某个j位二进
制数的阶码,可表示的指数为2^e=2^[2^j-1]然后把这个数转换成对应的以10为底的计数法表示出来(未知数已假设),m*2^e=c*10^d,解这个指数幂等式首先想到的是两
边取常用对数,得到log10(m)+e*log10(2)=log10(c)+d,先令左边为t,则d=t-log10(c),因为1<=c<10,所以log10(c)<1,因为d为指数,为正,所以d=t的取整。

#include <bits/stdc++.h> using namespace std; double M[10][31]; int E[10][31]; void la() { for(int i=0;i<10;i++) { for(int j=1;j<31;j++) { double m=1.0-1.0/(1<<(i+1)); int e=(1<<j)-1; double t=log10(m)+e*log10(2); E[i][j]=(int)t; M[i][j]=pow(10,t-E[i][j]); } } } int main() { double m; int e; la(); char s[105]; while(gets(s)&&strcmp(s,"0e0")) { for(int i=0;s[i];i++) if(s[i]==‘e‘) s[i]=‘ ‘; sscanf(s,"%lf %d",&m,&e); int f=0; for(int i=0;i<10;++i) { for(int j=1;j<31;++j) { if(fabs(M[i][j]-m)<1e-5&&e==E[i][j]) { f=1; printf("%d %d\n",i,j); break; } } if(f) break; } } return 0; }
原文:http://www.cnblogs.com/BobHuang/p/6798797.html