一,随机梯度下降法(Stochastic Gradient Descent)
当训练集很大且使用普通梯度下降法(Batch Gradient Descent)时,因为每一次\(\theta\)的更新,计算微分项时把训练集的所有数据都迭代一遍,所以速度会很慢
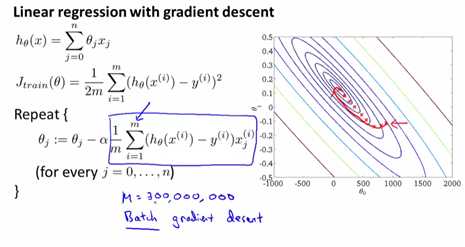
批量梯度下降法是一次性向计算m组数据的微分,一次更新\(\theta\),计算m组数据的微分时,用的是同一个\(\theta\),会获得全局最小值
随机梯度下降法依次计算乱序的m组数据的微分,m次更新\(\theta\),计算m组数据的微分时,用的是上一组数组更新完的\(\theta\),会获得非常接近于全局最小值的局部最小值
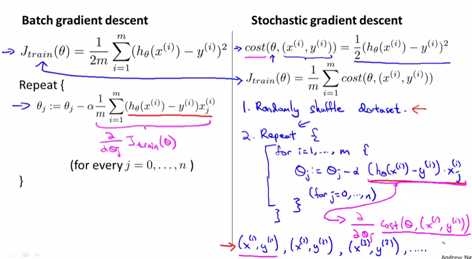
一般迭代1-10次
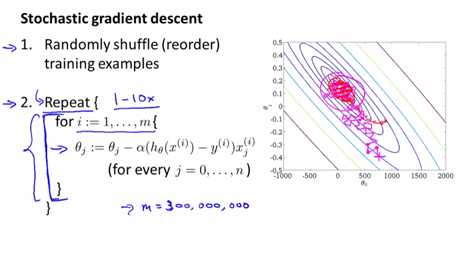
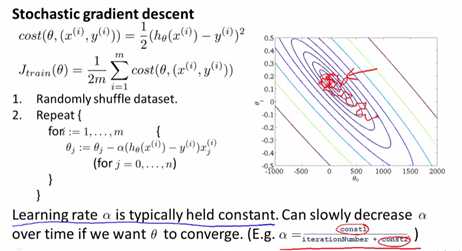
二,小批量梯度下降法(Mini-Batch Gradient Descent)
三种梯度下降法对比

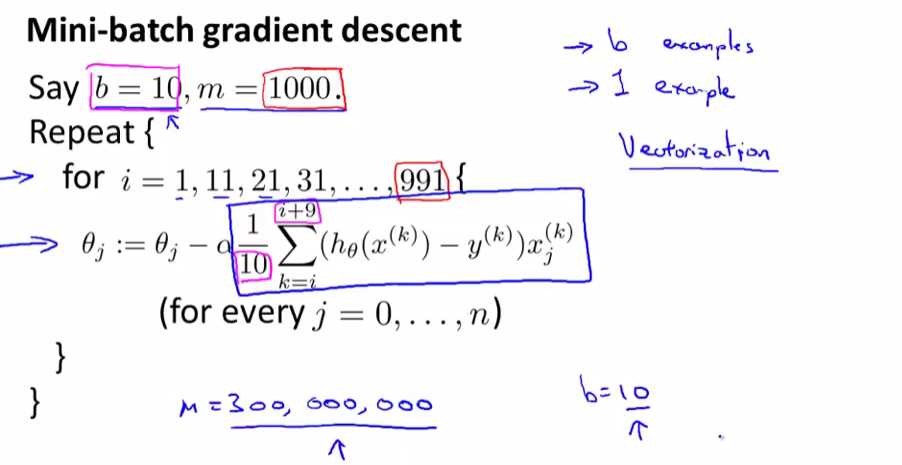
小批量梯度下降法就是一次更新b(一般是10,2~100d都可以)组数据,更新\( \lceil \frac{m}{b} \rceil\),介于随机梯度下降法和批量梯度下降法之间
小批量梯度下降法比随机梯度下降法速度快是因为更新\(\theta\)的频率快,比随机梯度下降法快是因为计算微分的时候可以向量化运算加速(即矩阵相乘)
三,验证代价函数收敛
在每次更新\(\theta\)前先计算\(Cost(\theta, (x^{(i)}, y^{(i)}))\)
因为随机梯度下降法每次更新\(\theta\),并不能保证代价函数\(Cost(\theta, (x^{(i)}, y^{(i)}))\)变小,只能保证总体震荡上变小,所以我们只需最近1000个数据\(Cost(\theta, (x^{(i)}, y^{(i)}))\)的平均值

上面两副图是比较正常的随机梯度下降图,下左需要提高样例数(1000->5000)再看看是否收敛,下右明显单调递增,选择更小的学习速率\(\alpha\)或者更改特征试试
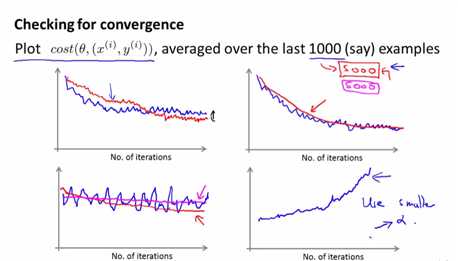
我们还可以动态修改学习速率来使代价函数收敛,随着迭代次数增加而减少
\(\alpha = \frac{const1}{iterationNumber + const2}\)
四,在线学习
在线学习就是在没有预先准备好的数据集的情况下,有数据流实时给予学习模型,实时更新\(\theta\),优点
1,不需要保存大量本地数据
2,实时根据数据的特征更改\(\theta\)
其实和随机梯度下降法类似

在线学习其他例子,可以根据用户搜索的关键词特征,来实时学习反馈结果,在根据用户的点击来更新\(\theta\),如

原文:http://www.cnblogs.com/xchaos/p/6827550.html